Special Relativity
The basic premise of the relativity is that no matter which frame of reference we consider, light always travels at the same velocity. Therefore, all frames of reference must be interchangeable.
(Einstein, 1916)In order to attain the greatest possible clearness, let us consider the example of the railway carriage supposed to be travelling uniformly. We call its motion a uniform translation ("uniform" because it is of constant velocity and direction, "translation" because although the carriage changes its position relative to an embankment yet it does not rotate in so doing). Let us imagine a raven flying through the air in such a manner that its motion, as observed from the embankment, is uniform and in a straight line. If we were to observe the flying raven from the moving railway carriage, we should find that the motion of the raven would be one of different velocity and direction than when observed from the embankment, but that it would still be uniform and in a straight line.
Expressed in an abstract manner we may say:
If a mass m is moving uniformly in a straight line with respect to a co-ordinate system K, then it will also be moving uniformly and in a straight line relative to a second co-ordinate system K', provided that the latter is executing a uniform translatory motion with respect to K. In accordance with the discussion contained in the preceding section, it follows that:
If K is a Galileian co-ordinate system, then every other co-ordinate system K' is a Galileian one, when, in relation to K, it is in a condition of uniform motion of translation. Relative to K' the mechanical laws of Galilei-Newton hold good exactly as they do with respect to K.
We advance a step farther in our generalisation when we express the tenet thus: If, relative to K, K' is a uniformly moving co-ordinate system devoid of rotation, then natural phenomena run their course with respect to K' according to exactly the same general laws as with respect to K. This statement is called the principle of relativity (in the special sense).
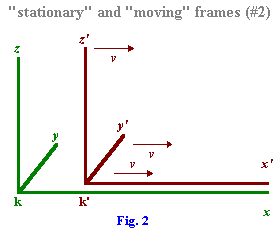
For the relative orientation of the co-ordinate systems indicated in fig. 2, the x-axes of both systems permanently coincide. In the present case we can divide the problem into parts by considering first only events which are localised on the x-axis. Any such event is represented with respect to the co-ordinate system K by the abscissa x and the time t, and with respect to the system K' by the abscissa x' and the time t'. We require to find x' and t' when x and t are given.
A light-signal, which is proceeding along the positive axis of x, is transmitted according to the equation
x = ct
or
x - ct = 0 ...(1)
Since the same light-signal has to be transmitted relative to K' with the velocity c, the propagation relative to the system K' will be represented by the analogous formula
x' - ct' = 0 ...(2)
Those space-time points (events) of (1) must also satisfy (2). Obviously this will be the case when the relation
(x' - ct') =l(x - ct) ...(3)
is fulfilled in general, where l indicates a constant; for, according to (3), the disappearance of (x - ct) involves the disappearance of ( x'-ct' ).
If we apply quite similar considerations to light rays which are being transmitted along the negative x-axis, we obtain the condition
(x' + ct') = m (x + ct) ...(4)
By adding (and subtracting) equations (3) and (4) we get:
2x' = lx + mx - lct + mct
x' = (l + m) x / 2 - (l - m) ct / 2
and
-2ct' = (l - m) x - (l + m) ct
ct' = (l + m) ct / 2 - (l - m) x / 2
By introducing for convenience the constants a and b, where
a = (l + m) / 2
and
b = (l - m) / 2 ,
we obtain the equations
x' = ax - bct
ct' = act - bx ...(5)
For the origin of K' we have permanently x' = 0, and hence according to the first of the equations (5)
x = bc t / a
If we call v the velocity with which the origin of K' is moving relative to K, we then have
v = x / t
v = bc / a
or
b = v a / c ...(6)
The same value v can be obtained from equations (5) if we calculate the velocity of another point of K' relative to K, or the velocity (directed towards the negative x-axis) of a point of K with respect to K'. In short, we can designate v as the relative velocity of the two systems.
Furthermore, the principle of relativity teaches us that, as judged from K, the length of a unit measuring-rod which is at rest with reference to K' must be exactly the same as the length, as judged from K', of a unit measuring-rod which is at rest relative to K. In order to see how the points of the x'-axis appear as viewed from K, we only require to take a "snapshot" of K' from K; this means that we have to insert a particular value of t (time of K), e.g. t = 0. For this value of t we then obtain from the first of the equations (5)
x' = ax.
Two points of the x'-axis which are separated by the distance dx' = 1 when measured in the K' system are thus separated in our instantaneous photograph by the distance
dx = 1 / a ...(7)
But if the snapshot be taken from K' at t' = 0, we get:
x' = a x - b c t
and
0 = a c t - b x
Therefore:
a c t = b x or t = b x / (a c)
Substituting we get:
x' = a x - b2 x / a
x' = a x ( 1 - b2 / a2)
Now, if we substitute for "b" (b = v a / c) , we obtain
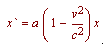
From this we conclude that two points on the x-axis separated by the distance 1 (relative to K) will be represented on our snapshot by the distance
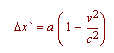 ...(7a)
...(7a)
But from what has been said, the two snapshots must be identical; hence dx in (7) must be equal to dx' in (7a), so that we obtain
dx' = dx
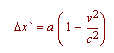 = 1/a = dx
= 1/a = dx
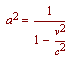 ...(7b)
...(7b)
The equations (6) and (7b) determine the constants a and b. By inserting the values of these constants in (5), we obtain the Lorentz Transformations.
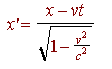 ... (8)
... (8)
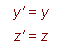 ... (8a)
... (8a)
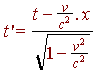 ... (8b)
... (8b)
Thus we have obtained the Lorentz transformation for events on the x-axis. It satisfies the condition
x' ² - c² t' ² = x² - c² t² ...(8c)
The extension of this result, to include events which take place outside the x-axis, is obtained by retaining equations (8) and supplementing them by the relations
y' = y
z' = z ... (9)
In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K' .
This may be shown in the following manner.
We suppose a light-signal sent out from the origin of K at the time t = 0. It will be propagated according to the equation
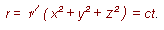
or, if we square this equation, according to the equation
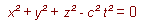 ...(10)
...(10)
It is required by the law of propagation of light, in conjunction with the postulate of relativity, that the transmission of the signal in question should take place -- as judged from K' -- in accordance with the corresponding formula
r' = ct'.
or,
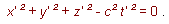 ... (10a)
... (10a)
In order that equation (10a) may be a consequence of equation (10), we must have
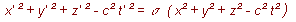 ... (11)
... (11)
Since equation (8a) must hold for points on the
x-axis, we thus have 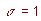 . It is easily seen that the
Lorentz transformation really satisfies equation (11)
for
. It is easily seen that the
Lorentz transformation really satisfies equation (11)
for 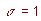 ; for (11) is a consequence of (8a) and (9),
and hence also of (8) and (9). We have thus derived the
Lorentz transformation.
; for (11) is a consequence of (8a) and (9),
and hence also of (8) and (9). We have thus derived the
Lorentz transformation.
The Lorentz transformation represented by (8) and (9) still requires to be generalised. Obviously it is immaterial whether the axes of K' be chosen so that they are spatially parallel to those of K. It is also not essential that the velocity of translation of K' with respect to K should be in the direction of the x-axis.
A simple consideration shows that we are able to construct the Lorentz transformation in this general sense from two kinds of transformations, viz. from Lorentz transformations in the special sense and from purely spatial transformations, which corresponds to the replacement of the rectangular co-ordinate system by a new system with its axes pointing in other directions.
Mathematically, we can characterise the generalised Lorentz transformation thus:
It expresses x', y', z', t' , in terms of linear homogeneous functions of x, y, z, t , of such a kind that the relation
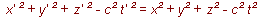 (11a)
(11a)
is satisfied.
That is to say: If we substitute their expressions in x, y, z, t , in place of x' , y' , z' , t' , on the left-hand side, then the left-hand side of (11a) agrees with the right-hand side.
Space and Time
From this it can be seen that there are four variables in this relationship, each of equal significance. Therefore time can be regarded as a dimension similar to the other three spacial co-ordinates. From equation (8b) it can also be seen that time is not measured the same in every frame of reference.
If we now consider some arbitary length Lo along the x-axis of the stationary frame, using equation (7a) and substituting for "a" it can be shown the the length L measured by the moving observer would be:
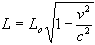 .... (12)
.... (12)
From the second of equations (5) if we consider a clock located at the origin of the fixed frame (x = 0) we see that:
c t' = a c t
t' = a t
If we now consider some arbitary time period to in the stationary frame, substituting for "a" in the equation above it can be shown the the time t measured by the moving observer would be:
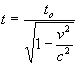 ...(13)
...(13)
Frequency Shifts
We observe that the frequency of light is related to the period of the light wave. The frequency of light is given by:
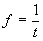
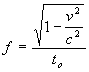
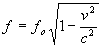 .....(14)
.....(14)
The frequency of a light signal as measured in the moving frame of reference will appear to be slower than in the stationary frame. This will appear as a Red Shift to the moving observer.
Mass - Energy
Now let us consider the case of a moving object, rather than a photon. Using Newton's law of motion:
F = m a
v = a t
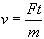
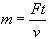
Now
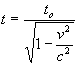
therefore 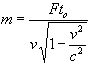
We will define 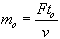 as the rest mass of an object.
as the rest mass of an object.
So
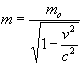 ............(15)
............(15)
Expanding this equation into a series gives:
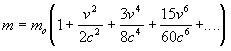
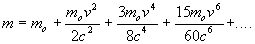 .........(16)
.........(16)
If v is small compared to c, the higher powered terms become so small in magnitude they can be ignored.
Therefore 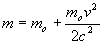
Now the kinetic energy of the object is 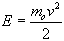
Therefore 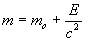
Neglecting higher terms in the equation:
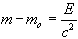
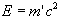 ...............(17)
...............(17)
where m' = the observed change in mass of the object.