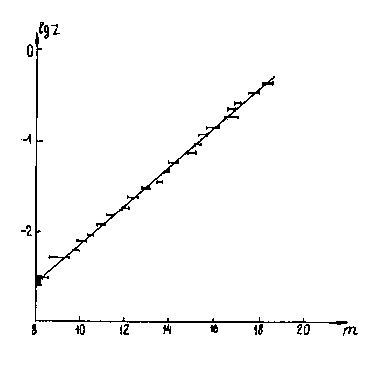
Fig.1 The experimental dependence of the visible stellar value of galaxies
from the red shift z. The straight
line corresponds to the function m(z) = 4.7 log z + 20.
(Received 26 August, 1987)
Abstract: A cosmological model is discussed which is based on interpretation of the speed of light with time everywhere in the Universe beginning with a certain moment of time in the past. The model is described by a metric in which the speed of light depends on time and the radius of the curvature of three-dimensional space remains constant (c-metric). It is shown that this metric leads to the same observed facts and formulas of different characteristics that the metric of standard cosmology does but with essentially different physical interpretation. Such a property is the consequence of conformity of spaces being defined by both metrics. The agreement with the fundamental physics laws is achieved by introducing the evolution of a number of other fundamental constants synchronously with the variation of the speed of light. The model considered connects the evolution of the universe with evolution of physical constants and permits explaining some unclear cosmological phenomena - for example, a high isotropy of the relict background and superluminal speed in quasars.
0. Introduction
The generally accepted model of the universe evolution is based on interpretation of the red shift by the radial speed of galaxies. Meanwhile, by the present time, suggestions have been published which explain the red shift by variation of different physical constants (the electron mass, the speed of light, etc., cf. Bellert, 1977; Mansfield and Malin, 1976).
The present paper considers the evolution of the speed of light as a cause of the red shift as well as a static cosmological model resulting from it (Troitskii). The red shift is explained by the hypothesis on continuous variation (decrease) of the speed of light in vacuum, beginning from a certain moment of time in the past everywhere in the universe. In Troitskii the consideration of the static cosmological model has been made on this basis. In order the evolution of the speed of light does not lead to the variation of the interaction constants, i.e., to the variation of the atomic spectra, nuclei stability and other regularities, the synchronous variation of a number of fundamental constants are accepted together with the light speed variation. A possibility of the fundamental constant variation was discussed previously beginning from Dirac, Gamov, Teller, etc., but it was not associated with the need to explain any known phenomena and was always practically in contradiction with the fundamental physical laws (see, for example, Chechev and Kamarovskii 1978).
The observed effects have been calculated using the space-time metric with varying light speed which are well correlated with the experimental data. The basic difference between the considered static cosmological model and the standard one is in the absence of the singularity of the universe dimension and the matter density at the initial moment of time. The constructed cosmological model corresponds to all known observed data. It permits explaining a high degree of homogeneity of the relict background and, in particular, admits the laboratory check.
1. Time-Space Metric with Varying Light Speed
We consider first the light propagation in material medium where the dielectric e and magnetic m permittivity are changed with time. The speed of light in this case is equal to c(t) = C0/n(t) where n(t) = Ö(em), C0 is the speed of light in vacuum. The medium is considered to be continuous, homogeneous, and isotropic. The equation of light propagation between two infinitely close points in the spherical reference system is
c2(t)dt2 - [dr2 + r2(sin2qdj2 + dq2)] = 0
In the medium is simultaneously compressed or broadening and the axis scale is changed together with it, i.e., the reference system accompanies the relative motion of the matter particles, then the differential interval between arbitrarily close events will be
dS2 = c2(t)dt2 - a2(t)[dr2 + r2(sin2qj2 + dq2)]
where a(t) is the scale factor, r is the dimensionless coordinates of particles. The spatial part of the metric is the Euclidean, since the finite (local) Physical space is considered. The above conditions may be created in the definite medium by the technical facilities available. The written metric equation shows the real condition of the light propagation in medium and the matter motion taking into account the relativistic effects (see, for example, Cherni, 1983). Naturally, the given metric may be used for the physical vacuum locally or for the whole visible space - i.e., to the metagalaxy. In this case it is necessary to consider the possible curvature of space. For the isotropic and homogeneous space-time in the synchronous reference system in the generally accepted form but taking into account the light speed variation, the interval will be
dS2 = c2(t)dt2 - d2(t)[dr2 + ¦2(r)(sin2dj2 + dq2)] , (1)
where r is the dimensionless radial coordinate of the matter, ¦(r) = sin r, sh r, r for the space of positive (k = +1), negative (k = -1), and zero curvature (k = 0), respectively, a(t) is the radius of the universe for k ¹ 0. When c(t) = c0 = const. has the metric of the standard cosmology which we shall call a-metric, for short. The metric for a(t) = a0 = const. we shall call c-metric and the general case of two scale factors ac-metric. The inherent (or real) time is defined by the space between two events in one and the same point of space, i.e., for dx1 = dx2 = dx3. For the general form of the interval record we have dS = Ö(g00dx0) where dx0 is the inherent time. For the metric (1) with the varying light speed is similar to dS = c(t)dt. If we compare the both expression we have dt = c(t)-1Ö(g00)dx0, but since in (1) g00 = c2(t), then dt = dx0. Thus, in the metric considered with the varying light speed the time dt is inherent.
2. Physical Interpretation of the Interval
In the general relativistic theory, GRT, the record of the interval with two scale factors of the form (1) is also used. However, in all papers a transformation to a new time t = òc(t)dt is made and further it is assumed silently that t just the time to be used by us. This transformation is proved by the fact that the physical laws do not depend on the coordinate system they are written down in. However, here is a citation on this idea in Landau and Lifshitz (1973): "In connection with the arbitrary choice of the reference frame, the laws of the nature are written down in the general relativistic theory in the form formally applicable for any four-dimensional coordinate system (or generally speaking in covariant form). This circumstance, however, does not denote the physical equivalence of all reference systems (similar to the physical equivalence of all inertial reference systems in the special relativistic theory). On the contrary, the concrete form of physical phenomena including properties of body motion becomes different in all reference systems."
The satisfied proof and examples of the phenomenon dependence on the coordinate system are given in Vladimirov (1982). Thus, intervals for c = c0 and c = c(t) are different in physical sense. However, for the case of controlled material medium the time part admits unequivocal interpretation, namely, that c0/n(t) is the varying light speed. In application to metagalaxy one, one may speak on two interpretations: on variation of the light speed in the form of c(t) = c0/n(t) where n(t0) = 1 and c0 is the light speed at the present epoch or on variation of the time rate d(t) = dt/n(t) with the constant light speed c0. In this case the inherent time is dt because c0dt/n = Ö(g00)dx0. We think that the assumption on variation of the time rate is better and corresponds to the idea of SRT and GRT. In reality, in SRT, time and space become relative equal coordinates in four dimensions of pseudo-Euclidean space. Yet, the scale of time and space in this four-dimensionality remains unchanged and, hence, the coordinates and time are linear. In GRT the space scale may be dependent on space and time, but the time-scale is unchanged. We may admit the following step in the frames of GRT ideas: assuming the nonlinearity of the inherent time rate together with the nonlinearity of spatial coordinates. This is equivalent to the admittence of existence of a peculiar cosmic time variation being nonlinear in time intervals of the metagalactic evolution and practically linear in its local regions, for example, in the galaxy scales apart from the solar system scales. We consider below the cosmological models following from (1) with both interpretations of the time part of the interval. All difference of interpretations is reduced to the fact that with the hypothesis of the real light speed variation one may consider variation of physical interaction constants, while with the hypothesis of the time-scale (rate) variation all the constants of interaction remain unchanged. The first case is much complicated, thus its analysis is the basic one. Here we restrict ourselves by the consideration of the static cosmological model being defined by metric (1) when a(t) = a0 = const.: i.e.,
dS2 = c2(t)dt2 - a02[dr2 + ¦2(r)(sin2qj2 + dq2)]
This metric is conformal to the metric of the standard cosmology, since it is obtained from the latter by multiplication of all its terms by a02/a2(t). Here the value in the time part of c02a02/a2(t) plays the role of c(t) = c0a0/a(t) = c0/n(t) where n(t) = a(t)/a0. As it is known, all distances and angles in both spaces are preserved. Simultaneously, conditions of light propagation defined by the zero geodesical ds = 0 remain identical. This means that the static model leads to the same relations associated with the light motion that the standard cosmology of the broadening universe does. We consider effects of the light propagation in the general case for the symmetrical metric when both scale factors take place.
3. Propagation of Electromagnetic Waves in Vacuum with Time-Variation Light Speed
Equation ds = 0 for the geodetic line-of-light in radial propagation gives from (1) for the dimensionless distance passing by light for the time from the moment of radiation t1 up to the moment of reception t0:
r(t0) - t(t1) = t1òt0[c(t)/a(t)]dt , (2)
If one wave oscillation emits from the point r(t1) with the period Dt1, in the time interval t1, t1 + Dt1 then the wave comes to the observation point in the time interval t0, t + Dt0. From (2) ways are found which the backward and forward wave fronts pass, taking into account their equality as well as smallness of intervals Dt1,0 during which a(t), c(t) may be considered unchanged, we have
[c(t0)/a(t0)]Dt0 = [c(t1)/a(t1)]Dt1 , (3)
Since Dt1 is the period of the emitted wave, then Dt0 will be the period of the received wave and turning into frequencies, we obtain
w1/w0 = [c(t1)/c(t0)][a(t0)/a(t1)] = z + 1 , (4)
where z is the generally accepted characteristic of the cosmological frequency shift, and w1 and w0 are the frequencies of the emitted and received oscillations, respectively. When a(t) = a0, i.e., for the static universe the frequency shift is defined by the variation of the speed of light
w0 = w1(1 - [c(t1) - c(t0)]/c(t1))
For sufficiently close periods of time t1 and t0, expanding a(t), c(t) into series near t1 in Dt = t0 - t1 we obtain
w0 @ wk[1 - (Hg - Hc)Dt] @ w1[1 - (Hg - Hc)(R/c0)] , (6)
Here Hg = (a•/a)t0 is the known expression for the Hubble constant in the stand cosmology and Hc = (c•/c)t0 = -n•/n in its analog at the varying light speed.
To explain the observed red shift due to variation of the speed of light one has to assume -Hc = H0 where H0 = 7 x 10-11 yr-1 is the modem value of the Hubble constant. From here, the rate of the light speed variation for a year amounts |c•| = H0c0 = 2 cm s-1 yr-1, of the time-scale equal to a year decrease by 3 ms year.
The effect of the red shift is obtained also in considering the light propagation by Maxwell equations, where e and m of the vacuum depend on time. For a plane wave we have
¶E/¶x = - ¶mH/¶t ; ¶H/¶x = - ¶eE/¶t
Using the method of solution given in Averkov and Ostrovskii (1958) for the case when e and m of the vacuum are changed with time synchronously over the similar law space becoming with the moment t = 0, we obtain
w = w1[c(t0)/c(t1)] , A0 = A1[c(t0)/c(t1)]
where A1 and A0 is the field amplitude of the emitted and received wave, respectively. The expression obtained for the red shift coincides with (4) for space-time characterized by c-metric.
For the emission having a solid spectrum we assume A12 = w1dw1, A02 = w0dw0 and taking into account that dw1/dw0 = c(t1)/c(t0) we have w0/c0 = w1/c1, i.e., with wave propagation the value w/c(t) = const. is preserved. From this solution it is that with the decrease of c(t) with time the wave energy decreases (red shift) and the increase of c(t) the wave energy increases (violet shift). In the case of material controlled medium the energy is taken from the controlling field (pump) or vice is given to it. In the application to the physical vacuum one must assume that the exchange takes place between the wave and vacuum.
The effect of the observed frequency variation in light propagation in vacuum varying speed has a simple explanation. The wavelength excited near the radii equal to l1 = Dt1c(t1). At the reception point for a(t) = a0 the metric wavelength conserves, but the light speed will be changed and being equal to c(t0); so this excites oscillation with the period T0 = l1/c0 = Dt1c(t1)/c0 and hence w0/w1 = c(t0)/c(t1) that coincides with the conclusion from the metric equation electrodynamic problem solution. This mechanism of the frequency variation considered Doppler with a difference that here there is no removal due to mechanical motion of the radiator, the distance remains constant geometrically, only the electric path length is changed L3 = t1òt0c(t)d(t), the dL3/dt = v = c(t0) - c(t1) and the Doppler shift will be w0 @ w1[1 - (v/c(t1))] that coincides with (5). In this case the transverse Doppler is absent as it must be.
At last it should be noted, that the considered mechanism of the red shift differs essentially from the suggested earlier explanation of the red shift due to the quantum aging: i.e., due to the energy loss with the propagation. According to the exponential law of the energy absorption in propagation, the quantum frequency must be exponentially changed with time: i.e., w0 = w1e-ar = w1e-ac0t = w1e-Ht. This case of the frequency dependence is the particular case of the general expression (5). It corresponds to the de Sitter idea of the exponential growth of the scale factor. As will be shown further, the function leading to the exponential frequency change does not satisfy observations.
4. The Red Shift and the Evolution of the Fundamental Constants
The value of the speed of light is a part of many physical regularities. Its variation results in variation of dimensionless constants of electromagnetic weak and strong interactions equal, respectively, to
ae = e2/hc , aw = gwme2c/h3 , as = gs2/hc
where e is a charge, me is the mass of an electron, gw is the Fermi constant, gs is the strong interaction constant and h is the Planck constant. This will effect atomic spectra, speeds of a and b decays, stability of massive nuclei and other processes of the nature.
At present, boundaries of possible variations of the given components (see, for example, Chechev and Kamarovskii, 1978; or Will, 1983) are experimentally defined. Tables I and II present these data. Discussion of the results may be found in Chechev and Kamarovskii (1978), Averkov and Ostrovskii (1958), Will (1983), Dyson (1971), Bahcall and Schmidt (1967), Tubbs and Wolff (1980), Shlyakhter (1976), Turnere and Stein (1976), Pochoda and Schwarzschild (1964), Gamov (1967), Dearborn and Schramm (1974), Van Flandern (1975), Shapiro (1982), Williams and Dicke (1976), Solheim, et al. (1976), Baum and Florentin-Nelson (1976).
TABLE I
| Year | Author | a•e/ae yr-1 | a•w/aw yr-1 | a•s/as yr-1 |
| 1971 | Dyson | 5 x 10-15 | 1 x 10-10 | 2 x 10-12 |
| 1967 | Bachall and Schmidt | 1.3 x 10-12 | - | - |
| 1976 | Shlyakhter | 4 x 10-11 | - | 2 x 10-12 |
| - | Shlyakhter | 1 x 10-17 | 2 x 10-12 | 5 x 10-19 |
| 1976 | Turnere and Stein | 4 x 10-12 | - | - |
| 1980 | Tubbs and Wold | 1 x 10-13 | - | - |
TABLE II
| Year | Author | G•/G yr-1 |
| 1964 | Pochoda and Schwarzschild | (4-7) x 10-11 |
| 1967 | Gamov | 4 x 10-11 |
| 1974 | Dearborn and Schramm | 5 x 10-11 |
| 1975 | Van Flandern | (8 ± 5) x 10-11 |
| 1975 | Rozenberg and Shapiro | (5-15) x 10-11 |
| 1976 | Williams and Dicke | 1 x 10-11 |
From expressions ae, aw, as it is seen that due to variation of the speed of light, dimensionless constants vary as |c•/c| = H0 = 7 x 10-11 yr-1. This is, by three orders of magnitude, larger than the determined variation boundaries of ae, aw, as. The permanence of the given constant may be satisfied if we assume the corresponding variation of the values e2, h, me, mp, qw, gs together with the speed of light. We accept also the condition of constancy in time for radiating spectra of hydrogen-like atoms including fine and superfine splitting. The corresponding frequencies will be
vnm = [maaa2/(ma
+ me)](mec2/h) , vLS = [maaa4/(ma
+ me)](mec2/h) ,
vJI = g2[maaa4/(ma
+ me)](me/mp)(mec2/h)
, (7)
where mp and ma are the masses of a proton and atom. The constancy of frequencies besides the permanence of a1 demands also the constancy of the Compton frequency vk = mec2/h and the mass relation me/mp. We suppose that the Newton force F ~ Gm2 must remain constant, that evidently, is experimentally confirmed (see, for example, Chechev and Kamarovskii, 1978; or Will, 1983).
From the above we find the time dependence of fundamental constants. For this we accept
e2 = e02cke~ ; h = h0ckh , m = m0ckm~ , gw = gw0ckw~ , gs2 = gs02cks~ , G = G0ckg~ , (8)
where ck = c(t)/c(t0) is the normalized light rate for the contemporary, its values c(t0) = c0, and e02, h0, m0... are the corresponding values of constants at present, here m, m0 refer to the mass of any particle. Powers e~, h~, m~ show the rate of variation of the corresponding physical constant in units c•/c = Hc, for example, m•/m = m~Hc, h•/h = h~Hc, etc. Substituting (8) in expressions of permanent constants we obtain values e~, h~, m~... g~ for which ae, aw, as, vk, and F remain constant (Table III).
Let us check now if the experimentally stated degree of the rate of a and b decay is provided for the found evolution of fundamental constants. One may conclude over estimations of radioactive isotopes abundance on the Earth and now on the Moon, that
TABLE III
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
the probability of a-decay - la if is changed then no more as by 10% for 109 years (Chechev and Kamarovskii, 1978). From here la|la £ 10-10 yr-1. The probability of a-decay with an accuracy up to unexisting coefficients is equal to
la = (v/2R)e-s
where v is the velocity of an a-particle, R is the dimension of the nucleus, S = 4pze2/vh, and z is the atomic number. If we find the logarithmic time derivative we obtain
la•/la = v•/v = -R•/R - S[(ae•/ae) + (c•/c) - (v•/v)]
For different nuclides the values S = 102-104 and, hence, variation of la are defined by parameters in the brackets. For S = 500 (for uranium) and la•/la x 10-10 yr-1 we obtain the condition
[(ae•/ae) + (c•/c) - (v•/v)] £ 2 x 10-13 yr-1
In what follows and from the value ae•/ae
(Table I), the indispensable demand v/c = const. follows. As we see below,
this condition takes place for the motion in space-time being described
by c-metric. Thus, in all variants of constant changes given by Table III,
variation of probabilities of a-decay is not
beyond the scope of permissible.
For b-decay in the presence of the electron
envelope
lb = (zM/50p)ae2aw2(mec2/h)(vmax/c)6
When vm/c = const. the probability of b-decay remains also constant. When vmax = const., lb•/lb = -6Hc that is not beyond permissible estimations of lb change with time.
5. Motion Of Particles
The inertia motion of a probe particle in four-dimensional space-time in the absence of a constant electric and magnetic field has the form
d2rs/dS2 + G(s/mv)(drmdrv/dSdS) = 0
where Gmvs is the Christoffel symbol. For the space given by ac-metric (1) in the radial motion when dj/dS = dq/dS = 0 using the known calculations of Gmvs, we obtain
d2t/dS2 + [(a•/a) + (c•/c)](dt2/dS) = (a•/a)(1/c2)
For a-metric we have the known in the standard cosmology equation and its solutions: va = const. For c-metric we obtain the solution v/c = b = const.; i.e., the particle inertial velocity is changed proportionally to the light rate. With varying time-scale vn(t) = v0 = const., i.e., the value vn(t)/c0 = b0 is conserved.
The particle pulse at the moments t0 and t1 is equal, respectively, to p0 = m0v0/Ö(1 - b2), p1 = m1v1/Ö(1 - b2), their relation p0/p1 = [c0/c1]m~ + 1. The kinetic energy at the moment t0, E0 = mcc02[(l - b2)1/2 - 1], its relation to the energy at the moment t1, E0/E1 - ck-m~ - 2. For the variant N3 of the constant evolution, which, as will be shown, satisfies in the best way the experience m~ = -2 and hence, p1 = p0c0/c1 and E0 = E1, i.e., the particle pulse increases with time and the kinetic energy remains constant. The latter denotes, in particular, the permanence of the Boltzmann constant that will be used in the next section.
6. Evolution of the Relict Radiation Background
At present t = t0, the spectral density of the relict radiation volume density is equal to
dw0/dw0 = (w02/p2c03)[(hw0)/(exp(h0w0/kT0) - 1)]
Substituting here the relations w0 = w1c0/c1 and h = h0(c1/c0)h~ we obtain the value of the spectral density in the past at the moment t = t1
dw1/dw = (w12/p2c13)[(h1w1(c0/c1)h~ + 1)/(exp(h1w1/kT0(c1/c0)h + 1 - 1)]
Making a comparison between the two expressions we obtain that the value T0(c1/c0)h + 1 = T1 takes the sense of the relict background temperature, T1, in the past. Here it is assumed that the Boltzmann constant in the space-time remains, unchanged, as
T1 = T0[c(t)/c0]h + 1 = T0(z + 1)h~ + 1 , (9)
At h = const. (h~ ~ 0) we get the known in the standard cosmology expression for T1. Integrating dw0, dw1 over all frequencies we are convinced that the energy density of the entire radiation in the past U(t1) and at present U(t0) = p2k4T04/15c03h03 are similar. This seems to be true to invariability of the universe volume at c-metric. It is seen that the photon pulse and the entropy are changed as
p1/p0 = (z + 1)h~ , S/S0 = (z +1)-(h~ + 1) , (10)
For the correlated with the experiment variant of the constant variation,
the photon pulse is unchanged and the entropy
increases with time.
7. Light Speed Dependence on Time
As calculations show the dependence character of the speed of light on time defines the red shift, the temperature of the relict background and other space-time parameters. The function c(t) plays the same role as the universe radius a(t) in the standard cosmology. However, at present, there is no theory and equation which would determine c(t) by the observed parameters. That is why the function c(t) has to be found over the best agreement of cosmological consequences with the observational data available. The red shift, the presence and value of the relict background, the density of the matter in the Universe, the abundance of the primary helium and finally, the dependence of the galaxy magnitude, their number and visible angular size on z are referred to these data.
Furthermore, we shall consider only the hot model, which permits explaining nucleosynthesis. In this case in (9) it must be h~ >> - 1, hence, c1/c0®¥ when t1 ® 0. The same condition, according to (5) is necessary for the horizon existence. One the basis of the given qualitative considerations, one may accept a simple function
c(t) = c0[t0/t]n , 0 £ t £ ¥ , (11)
where t0 is the present moment, i.e., the age of the universe. For this function the red shift will be observed in all the time intervals 0 £ t £ ¥ as for the open model in the standard cosmology. Substitution of the red shift by the ultraviolet one, i.e., the analog of the closed model (k = 1) is obtained if the periodic function c(t) is designated.
We consider such a class of functions c(t) which leads to the same laws of the light propagation in space-time with c-metric as in space-time with a-metric of the standard cosmology. According to this, for both spaces from metric (1) at ds = 0 we obtain two relations c(t)dt = a0dr(1) and c0dt = a(t)dr(2). If we assume dr(1) = dr(2) then geodetic lines of the light motion will be identical and the desired class of functions will be c(t) = c0a0/a(t), where a(t) is the Newtonian or Einstein solution for a(t). The obtained function c(t) (11) for n = 2/3 and n = 1/2 corresponds to solutions a(t) for models of the open Universe (k = 0) at the pressure p = 0 and p = e/3, respectively, where e is the energy density.
The above choice of functions c(t) = c0a0/a(t) denotes the conformal agreement of spaces of c-metric and a-metric. Table IV presents the corresponding functions c(t) in the parametric form obtained from the known solution a(t) for different space curvature k = 1, -1.0 and pressure p = 0, p = e/3. The table gives also functions accepted from the above physical assumptions including the exponential function of the de Sitter model. The pressure given in the table indicates only the origin of the function c(t).
Note that the condition c(0) = ¥ is not necessary, sufficiently to demand just large but finite value of c(0). In particular, the function (11) may be regularized, accepting c(t) = c0[t0/t + D]n, where D is the small value being chosen on the experimental basis.
Each of the functions c(t) given in Table IV defines the corresponding cosmological model. To state the real model we take the method adopted for the choice of models in the standard cosmology, i.e., by comparison of observed consequences with the experiment. We use the known tests of comparison between theoretical dependencies of the stellar value m and the visible angular dimension q of galaxies on z and observations. The test based on calculation of the dependence of the galactic number in the function of the radiation flux observed is considered to be insufficiently informative and is not used here. It should be noted, that the test q(z) in the standard cosmology is not practically used due to a serious contradiction with observations (see, for example, Legg, 1970).
8. Investigation of the Observable Consequences of the Model
As it is known, m = -2.5 log E where E is the energy flux from the galaxy at the observational point.
We assume that the source is an absolute black spherical body with the temperature T. The spectral density of the radiation flux from all the surface pl2/4 in the unit of the solid angle is equal to
dw = (pl2/4)[w12/4p2c2(t1)][h1w1dw1/(exp(h1w1/kT1) - 1)] , (12)
Luminosity, which this flux creates at the observational point being at the distance R(z), is defined by the area of the spherical surface R2(z) connecting the single solid angle with the centre in the source as well as by variation of constants c(t) and h(t) for the time of fight propagation t0 - t1. Substituting w1/w0 = z + 1; h = h0(z + 1)h~; c(t1)/c(t0) = z + 1 into (12) and dividing by the area R2(z) we shall have for the illumination
dE = [pl2w02/16p2R2(z)c2(t0)][h0w0(z + 1)h~ + 2dw0/exp[hw0(z + 1)h~ + 1/kT] - 1] , (13)
Integrating over all frequencies we obtain
E = L/R2(z)(z + 1)3h~ + 2 , (14)
where
L = (pl2/4)[p2k4T4/60c02h03]
is the energy flux from the galaxy in the unit of the solid angle at the moment of the radiation t = t1. The term (z + 1)3h~ is associated with the effect of h variation, the (z + 1)2 takes into account the quantum attenuation by (z + 1) times and the rease of the quantum flux density in the same degree due to the red shift. Substituting (14) into the expression for m and taking into account that -2.5 log L = M - 5 is the solute stellar value of the galaxy at the radiation moment we obtain
m = M - 5 + 5 log(z + 1)R(z) + 7.5h~ log (z + 1) , (15)
TABLE IV
| No. | p | k | c(t) | R0 | q0 | R(z) = (c0/H0)y(z)
m(z), q(z) |
| 1 | 0 | 0 | c(t) = [c0(t0/t)2/3]/(0 £t £ ¥) | c0/H0q0 | 1/2 | q(z, 0) = l/R(z, 0)
R(z, 0) = c0/H0[zq0 - (1 - q0)(Ö(2zq0 + 1) - 1)]/[(z + 1)q02] |
| 2 | 0 | 1 | c(h) = c0[(1 - cos h0)/(1
- cos h)] ;
t = a0/c0[(h - sin h)/(1 - cos h0)] 0 £ h £ 2p |
c0/H0q0 | 1/2 £ q0 £ ¥ | m(z, 0) = 5 log (z + 1)y(z, 0) +
B
B = M + 43 - log h + 7.5h~ log (z + 1) |
| 3 | 0 | -1 | c(h) = [c0(ch h0
- 1)/(ch h - 1)] ;
t = a0(sh h - h)/c0(ch h0 - 1) 0 £ h £ ¥ |
c0/H0q0 | 0 £ q0 £ 1/2 | |
| 4 | e/3 | 0 | c(t) = c0(t0/t)1/2
0 £ t £ ¥ |
c0/H0Ö(q0) | 1 | q(z, e/3)
= l/R(z, e/3)
R(z, e/3) = c0H0[(Ö(q0z2 + 2q0z +1) - 1)/((z + 1)q0)] |
| 5 | e/3 | 1 | c(h) = (c0sin h0)/(sin
h)
t = a0(1 - cos h)/c0(sin h0) ; 0 < h < p |
c0/H0Ö(q0) | 0 £ q0 < ¥ | m(z, e/3) = 5 log (z + 1)y(z, e/3) + B |
| 6 | e/3 | -1 | c(h) = (c0sh h0)/(sh
h)
t = a0(ch h - 1)/c0(sh h0) ; 0 £ h £ ¥ |
c0/H0Ö(q0) | 0 £ q0 £ 1 | |
| 7 | 0 | c(t) = c0(t0/t)1/3
0 £ t £ ¥ |
c0/2H0 | 2 | R0(z) = (c0[(z + 1)2 - 1])/2H0(z
+ 1) ;
m(z) = 5 log [(z + 1)2 - 1]/[2(z + 1)] + B |
|
| 8 | 0 | c(t) = c0(t0/t)1/2
0 £ t £ ¥ |
c0
H0 |
1 | R0(z) = (c0/H0)[z/(z + 1)]
;
m(z) = 5 log z + B |
|
| 9 | 1 | c(t) = c0(t0/t)1/2
0 £ t £ ¥ |
(c0/H0)(2/p) | 1 | R2(z) = (c0/H0)(2/p)[sin
(p/2)][z/(z + 1)] ;
m(z) = log [(z + 1) ln(z + 1)] + B |
|
| 10 | 0 | c(t) = c0(t0/t)1
0 £ t £ ¥ |
¥ | 0 | R0(z) = (c0/H0)[ln(z + 1)]
;
m(z) = log [(z + 1) ln(z + 1)] + B |
|
| 11 | 0 | c(t) = c(0)(t0/t)2
0 £ t £ ¥ |
¥ | -0.5 | R0(z) = 2(c0/H0)[Ö(z
+ 1) - 1] ;
m(z) = 5 log 2[Ö(z + 1) - 1] + B |
|
| 12 | 0 | c(t) = c(0)e-H0t
0 £ t £ ¥ |
¥ | -1 | R0(z) = (c0/H0)(z) ;
m(z) = 5 log z(z + 1) + B |
The visible angular dimension of the galaxy in the considered static model is equal
q = l/R(z) , (16)
where l is the linear dimension of the galaxy at the radiation moment, and R(z) is the distance up to the galaxy at the observation moment equal to the distance passed by light for the time from the radiation up to observation t0 - t1.
We will now find an expression for distances R(z) in space-time given by c-metric. Substituting in (2) a(t) by a0 we obtain an expression for dimensionless radial distance points and t0 of the form
r = (1/a0)t1òt0c(t)dt , (17)
The distance in length units depends on curvature and is equal to R(z) = a0¦(r) where ¦(r) = sin r, sh r, r, respectively for k = 1-1.0. Substituting in (17) an expression for c(t), from Table IV we yeild at k = +1-1.0, respectively,
R + (z) = a0sin(h0 - h1) ; R - (z) = a0sh(h0 - h) ; R0(z) = a0(h0 - h1) , (18)
let us express the given distance by z.
For this we use the following relations: a relation between the speed of light at the moment t1 and the speed at moment t0, c(h1)/c(h0) = z + 1, the value of the Hubble constant at the present moment H0 = (c•/c)t0 and the function 1/c(t) curvature, or otherwise, deceleration of the inverse value of the speed of light
q0 = (1/c)[(d/dt)(1/c)]-2(d2/dt2)(1/c)
As an example we give a calculation of R for the function c(t) when p = 0 and k = 1, -1, 0. For the case k = +1,
c(h1)/c(h0) = (1 - cos h0)(1 - cos h1) = z + 1 , |Hc| = (c0/a0)[sin h0/(1 - cos h0)] ; q0 = 1/(1 - cos h0)
From the latter relation it is seen that q0 may be changed in the limits 1/2 £ q0 £¥. Transforming h, h0 in (18) by the obtained relations we shall get R(z) for the functions of the group p = 0, k = 1, 0, -1.
R(z, p = 0) = [c0/H0q0(z + 1)][z + ((q0 +1)/q0)(Ö(2q0z + 1) - 1)] , (19)
where 1/2 < q0 < ¥ for
k = 1; 0 < q < 1/2 for k = 1.
This expression coincides with the formula obtained in the standard
cosmology by Mattig but in different ways (cf. Mattig, 1958). The analogous
calculations of R(z, p = e/3) for c(t) corresponding
to the pressure p = e/3 and k = 1-1.0 gives
R(z, p, e/3) = [c0/H0q0(z + 1)][Ö(z2q0 + 2zq0 + 1) - 1] , (20)
where 1 < q0 < 1, k = 1, q0 = 1, k = 0.
For z ® ¥
we obtain the radius R0 of the universe and its lifetime. According
to (19) and (20),
(p = 0)R0 = c0/H0q0 ; t0 = 1/H0q0 ; (p = e/3)R0 = c0/H0Ö(q0) , t0 = 1/H0Ö(q0) , (21)
It is seen that in calculating R(z) using the scale time function we get just the same relations. The corresponding expressions for m(z) and q(z) obtained on the basis of calculations carried out are shown in Table IV.
Of importance is the fact that for c-metric with the given function c(t) but with different curvature of three-dimensional space k = +1-1.0, the curves m(z) for 0 < z £ 1 are practically completely indistinguishable and are only slightly diverged up to z ® ¥. One may be convinced of this by an example given in lines 8, 9 of Table IV. Thus, the character of curvature of three-dimensional space is extremely weakly influences on the functions m(z), q(z), i.e., finally on conditions of light propagation which define these dependencies.
9. Comparison of m(z) and q(z) Curves with Observational Data
Figure I shows an experimental curve m(z) being drawn by the least-square method through points. Each is the mean value of measurements of 6-8 galaxies known by the present time. The experimental function is well described by the straight line m(z) = (4.7 ± 0.1) log z + 20. The theoretical dependencies m(z) obtained in Table IV are given together with experimental points in Figure 2. All theoretical curves of Figure 2 for the exception of the right curve are built for h~ = 0, i.e., h = const. An effect of evolution of the Planck constant is illustrated by the curve for q0 = 1 (the fourth line of the table) built both for h~ = 0 and h~ = 2. From the figure it is seen that the curve q0 = 1, h~ = 2 is strongly deviated to the right from the curve q0 = 1, h~ = 0 and experimental data. All the remaining curves would be shifted to the right in the same manner for h~ = 2. One may conclude that the dependencies for h = 0 better satisfy observations m(z). Under this condition the best agreement with the experiment without consideration of evolution effects is obtained at q0 @ 2 for c(t) written in lines 2, 5, 7 of Table IV.
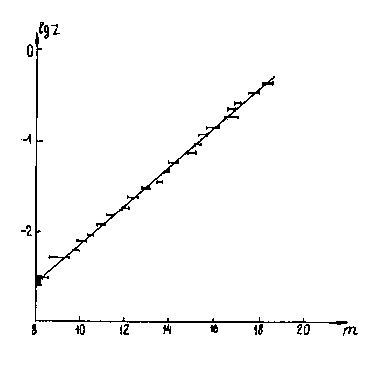
Fig.1 The experimental dependence of the visible stellar value of galaxies
from the red shift z. The straight
line corresponds to the function m(z) = 4.7 log z + 20.
Figure 3 presents a comparison between theoretical curves q(z) and observations of dual systems. Points are visible dimension of galaxies, crosses that of quasars. The theoretical curves are built both over formula of the present paper (solid lines) and over formula of the standard cosmology (dotted lines) for the distance between components l = 400 kpc. This corresponds to the upper boundary of the experimental data spread which are supposed to be undistorted due to the base line projection of double sources on the direction of observation.
From Figure 3 it is seen that the theoretical curve of the standard cosmology contradicts to the experiment, while a good agreement for q0 = 1-0.5 takes place for the model considered. However, in both tests, values of q0, are slightly diverged. This divergence may be satisfactorily explained by the evolution effect. The decrease of the slope dm/d log z from 5 up to 4.7 may be induced by the decrease of the galaxy luminosity with time. A correction for this effect in the form M(z) = M0 + 0.5 + 0.3 log z for 10-2 £ z £ 1 leads the experimental curve to the coincidence with the theoretical one when q0 = 1 ± 0.3, having an equation m(z) = 5 log + 20.5. Here we obtain the decrease of the absolute value of the stellar magnitude dM/dt @ -0.05 x 10-9 stellar mag yr-1, that is well correlated with estimations available. A correction for the evolution of q(z) is associated with an assumption on dimension increase of dual systems with time. Consideration of the dimension by 1.5 times for 1010 years is sufficient for the coincidence of the experimental data and the theoretical curve q(z) at q0 = 1.
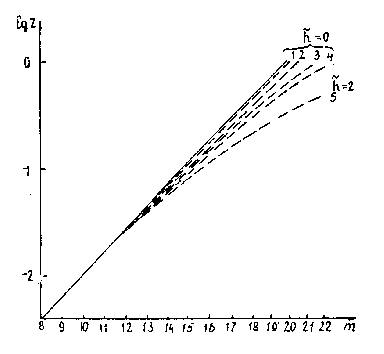
Fig. 2 A comparison with observations of theoretical dependencies of
the stellar value m of galaxies on
the red shift z. The solid curve is observations, dotted curves are
the theoretical data:
Thus, both tests give q0 = 1 ± 0.3 that corresponds to space with cyclical or noncyclical variation of the speed of light. The tests m(z) and q(z), with taking account of evolution, sufficiently and definitely lead to a model with the function of the light speed variation
c(t) = c0(t0/t)1/2 or c(h) = c0[(1 - cos h0)/(1 - cos h)] ; t = [(a0h - sin h)/(c0(1 - cos h0))] for q0 = 1
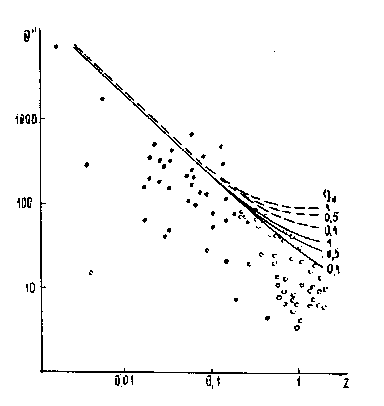
Fig. 3 A comparisonbetween observations and theoretical dependeces
of the visible angular dimension of binary systems of 400 kpc on the red
shift. Solid curves: for the model with the light speed evolution; dotted
one: for the model of the standard cosmology. Dark circles: observational
data for galaxies; light circles: for quasars.
From Table III it is seen that the requirement that h~ = 0 gives the following character of constant variations
h = const., m(t1) = m(t0)(c1/c0)-2, e2(t1) = e2(t0)(c1/c0) , G(t1) = G0(c1/c0)4 , (22)
An expression for the mass variation is equivalent to m1c12 = m0c0 = const. - i.e., in the evolution process the energy conservation law in space-time, defined by c-metric, is kept. Therefore, the total energy of the whole mass and that of the relict radiation in the universe is constant and equal to E0 = M0c02 + VU(t0) where V is the volume of the universe.
If we know the function c(t), it is not difficult to find from (9) the function of the relict radiation temperature. Adopting the expression c(t) - c0(t0/t)n for n = 1/3, 1/2, 2/3 and t0 = 1.5 x 1010 yr, we have
T1/3 = (2 x 106)/(t3/2) ; T1/2 = (1.7 x 109)/Ö(t) ; T2/3 = (1.5 x 1012)/(t2/3) , (23)
where t is in seconds. An expression for T1/2 coincides with an ordinary, given formula of the temperature in the standard cosmology. The same relations have been obtained when the light speed is constant. Hence, the fundamental constants are permanent, but the time-scale is changed.
10. Density of Matter in the Universe
In the standard cosmology the red shift is unambiguously defined by gravity forces that permits us to connect the matter density with the Hubble constant.
In our case, for the estimation of the matter density we use the condition of the electromagnetic radiation retention by the gravity field. We have obtained that at the initial moment the universe consists entirely of the electromagnetic radiation at a very large velocity of its propagation and a high temperature. The total energy of this radiation is finite and equal to E0 = M02 = VU(t). At an infinitely large light speed this energy must be instantly scattered.
Limitation and constancy of the electromagnetic field volume are possible under the condition that the field is distributed in space limited by the gravitational radius Rg. For this it is necessary that
2G(0)E0/c4(0) = Rg = R(0) , (24)
where R(0) is the initial radius of the universe. Easy to see, using (22) that Rg remains permanent in the process of constant evolution. Then, the modem radius of the static universe R0 = R(0) = Rg, i.e., it is a closed system with the curvature radius R0 = Rg and the volume V = 2p2R3(0). Substituting E0/c2(0) = M(0) = 2p2R3(0)r(0) in (24) we obtain r(0) = c2(0)/4p2G(0)R2(0). Further, using (22) we express the initial values of parameters by their modem values. As a result we have time-independent relations for the present density of matter for the present values of constant r0 = c02/4p2G0R02. Values c02 and R02 are related by Equation (21), i.e., by the value R(z) when z ®¥. According to (21), R0 = c0/H0Ö(q0), and finally
r0 = (H02q02)/(4p2G0) , r0 = (H02q0)/(4p2G0) , (25)
When q @ 1 the matter density in both cases by 3p/2 @ 5 times less than the estimation of the critical density, being 10-29 g cm-3 in the standard cosmology. According to the relation obtained, the modern density of matter in the universe for M0 = 75 km s-1 MPS r0 = 2 x 10-30 g cm-3. It is stated that the mean matter density in the Universe is no less than 5 x 10-31 g cm-3.
11. Evolution of the Static Universe at the Initial Period
The above calculations show that at the initial moment the Universe was a closed space with almost the same dimensions or equal to the present one, filled by the electromagnetic radiation, having practically large temperature and the speed of propagation.
The speed of light c(0) sufficient to explain the process of nucleus synthesis, as (9) shows, amounts c(0) = 1010c0 and may be considered practically infinite. Then according to (22), at the initial moment the particle mass and, hence, the matter density amount 10-20 of the modem mass and density, and the charge of an electron and the gravitational constant will be, respectively, by 105 and 1040 times larger than the present values. In explanation by the time-scale factor the given constants are unchanged, but the time-scale is variable. The energy density of the electromagnetic radiation at the initial moment is equal to its modem value E0/V = r0c02 + U(t0) and its mass density E0/VC2(0) due to a large speed of light c(0) is close to zero. Thus, the singularity of the matter density at the initial moment is absent.
Due to a large speed of light or a large value of the time-scale factor, n-1(t), at the initial moment the interval of events will be entirely time-like. This means that all events in the universe are practically simultaneous - i.e., it is as if compressed in a point, or otherwise due to a large value of |Hc| = t-1 for t = 0, the horizon of events is very small. When time passes, the horizon increases with the speed of light - i.e., for very small t it increases approximately as c(0)t. Hence, the matter density and the mass density of the relict radiation increase according to E0/VC2(t) and the total energy density remains constant and the energy-pulse tensor is invariable with time.
We have described the original state at the initial moment and the direction of evolution. But a question is raised: is it possible to make any well-founded logical conclusion on the mechanism and causes of this state occurrence? Answers to this question cannot be given on the basis of the models considered.
One may suppose, that if the Universe consisted of the electromagnetic radiation at the initial moment, then it is originated by generation of the electromagnetic radiation. For example, at the initial moment, a finite portion of the energy equal to E0 was radiated in a certain large or small volume.
Due to a large speed of propagation, the radiation practically occupied instantly a certain volume, being defined by the gravitational radius of the emitted portion of energy equal, as we see, to 2c0M0/c02 - the present gravitational radius of the universe. In order for a sufficiently quick filling to take place, we may choose such a function c(t), for example, with a plane section close to t = 0 that light has time to speed the universe for a year. For this, it is sufficient that c(0) @ 1010. This scenario is similar to the so-called inflation theory. It is also close to the hypothesis on the universe formation due to the phase transition of the physical vacuum state.
12. Discussion of Results
The basic difference between cosmology in terms of the hypothesis on the light speed variation is in the fact that the moving force of evolution of the universe in the standard cosmology is the gravitation alone, while in the considered one the phenomenon of the electromagnetic interaction as well. The analysis carried out shows that hypotheses explaining the red shift either by variation of the speed of light or variation of the time-scale give similar cosmological models. However, the acceptance of the first one demands the introduction of evolution of a number of other fundamental constants. As a result, besides the agreement of the constant variation with the basic regularities of physics, a question arises on compatibility of the hypothesis and the present paper with SRT, GRT, electrodynamics and relativistic mechanics. An agreement with GRT is defined by the use in the paper of generalized curvilinear coordinates, methods and formula of GRT. The metric considered is correlated with SRT in the same way as the metric of standard cosmology, i.e., it is Lorenz-invariant only locally.
However, irrespective of our analysis, would the introduction of the evolution of the speed of light be in contrast with the SRT? Note that SRT is based on experimentally stated invariance of electromagnetic phenomena and speed of light in moving inertial reference systems. Mathematically it is written down by the interval invariance in pseudoEuclidean space where the speed of light is considered to be constant. Here, the Lorenz transformation provides the constancy of electromagnetic phenomena in transitions to different inertial systems being at any distance from each other both in space and time. The introduction of the evolution of the speed of light excludes the possibility of the Lorenz transformation between inertial systems being far from each other. With the evolution of the speed of light the Lorenz-invariance would take place only for systems of reference, placed limiting and time intervals where the speed of light may be assumed to be practically constant. The transition from one reference system to the other for large intervals is made by GRT methods that were done in the paper in finding out the red shift effect.
Note that the Maxwell equations remain valid and their solutions at any concrete value of c(t) are true in all space with given properties. It is evident here, that measurement of the speed of light by observers in different inertial systems being in the limits of local region gives the similar value corresponding to the given time-scale. Thus, each of the observers obtain one and the same function c(t) during lasting measurements. In considering processes at large time and space intervals, the definition of inertial motion is somewhat different. If, in the classical and relativistic physics, the inertial motion is a relative motion with the constant velocity v or the general one with the unchanged energy, then in space, with varying light speed, the inertial motion as was shown is the motion with v/c(t) = b = const. In this case and taking account of mc2 = const., the energy of a moving body equal to E = mc2/Ö(1 - b2) remains also unchanged. So, the energetic definitions of the inertial motion in pseudo-Euclidean space with the constantcy of the speed of light and variable are coincided. As for other relations of the relativistic mechanics, for example, the pulse, then with that definition of the inertial motion the pulse p = mv/Ö(1 - b2), where v = bc will be changed as p•/p = c•/c = H0 @ 10-18 s-1. Additional terms occur in equations of the relativistic dynamics. Their relative value will be of the order of 10-18 than is by ten orders of magnitude less than the limit of accuracy of any laboratory measurements of mechanic values and, hence, this correction is at present indefinable neither in science nor in practice. So, the metric with varying light speed and time rate may be considered pseudo-Euclidean for the mechanics in space-time-scale of ordinary and scientific activity. Appreciable effects associated with variation of the speed of light may be noted only in scales of the universe lifetime. This situation in a definite sense is similar to one occurred in the introduction of a A-term.
If we accept the hypothesis on the time-scale variation then problems with variation other constants no longer arise and the rest ones are conserved, but they are the same with the light speed variation.
The cosmology on the basis of the hypothesis of the speed of light or time-scale variation permits to explain to be not in cosmological contrast with the modern physics such observed phenomena as red shift, hotizont, relict background, matter density, dependence of the visible value of galaxies on z, etc. Moreover, the suggested model is one to explain the observed dependence of the visible angular dimension of galaxies on z, as well as a large degree of large-scale homogeneity of the relict background. A large speed of light or a large time-scale at the initial moment provides the energy change in the scale of all universe and, hence, the ideal homogeneity of the background. An essential peculiarity of the new model is the principle possibility of its laboratory check. It seems that a proper method would be the speed of light measurement e material length standard and the suitable time standard. However, with variation constants the material standard length may also change. In reality, with the stated character of constant variation (22) the Bohr radius of an atom r = h/mc2 and the dimension of an electron re = e2/mc2 are changed as r•/r = c•/c, hence, the length of the material standard will be also changed in the same manner. That is why the light speed measured in this way remains unchanged.
We consider the light speed measurement with the use of length and time standards. length standard is the wavelength of krypton line and the time standard is the oscillation period of hydrogen and cesium oscillators. According to (7) the standard length is equal to lkr = c/vnm = bhc/mec2ae where b = (ma + me)/ma@ 1 the standard time is q = vjI-1 = bmph/me2c2ae4ge. If the hot ray passes the distance Nlkr. for the period Mq, then the unknown light speed is equal to c = Nlkr/Mq where Ö(N/M) = ae-1Ö(mp/mege). The variation of the ae may be observed for a comparatively small interval of time of the order of 10 years.
It should be noted, that one need not expect variation due to the constant evolution of the natural rotation of bodies (planet, pulsars). In reality, the conservation of the moment J = mr2W requires that J•/J = m•/m + 2r•/r + W•/W = 0, substituting here m•/m = 2H0 and r•/r = c•/c = -H0 from (22) we get W•/W = 0 - i.e., the effect of the increase is compensated by the decrease of the linear dimension of the body.
The considered cosmological model of the static universe meets a number of points. Gravitational forces begin acting at once after the sphere formation which is filled by the electromagnetic energy, then this must lead to the beginning of the universe recession from the very first moment t = 0. This may be admitted if the violet shift is compensated by the corresponding decrease of c(t) as it is seen from equations (4)-(5). It is physically more probable, that processes of the speed of light variation and broadening and compression of the universe may be causally connected. three models of the universe may be developed on the basis of the hypothesis fight speed variation: (1) the static model with the decrease in the speed of light, (2) the compressed one with the decrease in the speed of light, and (3) the broadening one with increase or decrease of the speed of light.
References
Averkov, S. 1. and Ostrovskii, L A.: 1958, Izv. VUZov, Radloflzika
1,
No. 4, 46.
Bahcall, J. M. and Schmidt, M.: 1%7, Phys. Rev. Letters 19,1294.
Baum, W. A. and Florentin-Nelson, R.: 1976, Astrophys. J. 209,
319.
Bellert, S.: 1977, Astrophys. Space Sd. 47, 263.
Chechev, V. P. and Kamarovskii, Ya. M.: 1978, Radioactivity and
Evolution of the Universe, Nauka, Moscow.
Chernyi, L T.: 1983, Relativistic Models of Solid Media, Nauka,
Moscow.
Dearborn, D. S. and Schramm, D. N.: 1974, Nature 247, 441.
Gamov, G.: 1967, Proc. Nat. Acad Sd. 57, 187.
Landau, L D. and Lifshitz, E. M.: 1973, 71teReld Themy, Nauka,
Moscow.
Legg, T. H.: 1970, Nature 226, 65.
Mansfield, V. N. and Malin, S.: 1976, Astrophys. J. 209, 335.
Mattig, W.: 1958, Astron. Nachr. 284, 109.
Pochoda, P. and Schwarzschild, M.: 1964, Astrophys. J. 139,
587.
Shapiro, 1.: 1982, AsnVhysics, Quantum and Reladvistie Theory,
MIR,
Moscow, p. 215.
Shlyakhter, A. 1.: 1976, Nature 264, 340.
Solheim, J. E., Bames, T. G., and Smith, H. J.: 1976, Astrophys.
J. 209.
Troitskii, V. S.: Dokl. Akad. Nauk USSR 290.
Tubbs, A. D. and Wolff, A. M.: 1980, Astrophys. J. 236,105.
Turnere, J. P. and Stein, S. R.: 1976, An Experimental Limit
of
the
Time Variation of the Fute Structure
Constants, Atom. Masses.
Van Flandern, T. C.: 1975, Monthly Notices Roy. Astron. Soc.
170,
333.
Vladimirov, Yy. S.: 1982, Reference Systems in the Gravitational
Theory, Energoizdat, Moscow.
Will, K. M.: 1983, in M. Hawking (ed.),'Gravitational Theory and Experiment,
General
Relativistic Theory,
MIR, Moscow.
Williams, J. G. and Dicke, R. H. et al.: 1976, Phys. Rev.
Letters 36, 55 1.
Note: You may need to set font preferences on your web browser for the equations to read correctly. Windows fonts are preferable.
June 6, 1999. Transcribed and converted to HTML by Derek Miller (jester@ix.netcom.com).
Back to Velocity of Light Pages
Back to Lambert Dolphin's Library