General Relativity
Special Relativity is the study of behaviour in uniformly moving frames of reference. Now let us consider the situation for an accelerating frame of reference.
We will now revisit Einstine's famous thought experiment.
(Einstein, 1916)Imagine a large portion of empty space, so far removed from stars and other appreciable masses, that we have before us approximately the conditions required by the fundamental law of Galilei.
It is then possible to choose a Galileian reference-body for this part of space (world), relative to which points at rest remain at rest and points in motion continue permanently in uniform rectilinear motion. As reference-body let us imagine a spacious chest resembling a room with an observer inside who is equipped with apparatus.
Gravitation naturally does not exist for this observer. He must fasten himself with strings to the floor, otherwise the slightest impact against the floor will cause him to rise slowly towards the ceiling of the room.
To the middle of the lid of the chest is fixed externally a hook with rope attached, and now a "being" (what kind of a being is immaterial to us) begins pulling at this with a constant force. The chest together with the observer then begin to move "upwards" with a uniformly accelerated motion. In course of time their velocity will reach unheard-of values -- provided that we are viewing all this from another reference-body which is not being pulled with a rope.
But how does the man in the chest regard the process?
The acceleration of the chest will be transmitted to him by the reaction of the floor of the chest. He must therefore take up this pressure by means of his legs if he does not wish to be laid out full length on the floor.
He is then standing in the chest in exactly the same way as anyone stands in a room of a house on our earth.
If he release a body which he previously had in his hand, the acceleration of the chest will no longer be transmitted to this body, and for this reason the body will approach the floor of the chest with an accelerated relative motion. The observer will further convince himself that the acceleration of the body towards the floor of the chest is always of the same magnitude, whatever kind of body he may happen to use for the experiment.
Relying on his knowledge of the gravitational field, the man in the chest will thus come to the conclusion that he and the chest are in a gravitational field which is constant with regard to time.
Therefore, by the principle of equivelance, because a gravitational field produces an acceleration, it can be regarded as an accelerating frame of reference. So the relationships within a gravitational field can be used to describe the behaviour of any accelerating frame of reference.
If a particle, initially at rest at a distance r from a mass is allowed to fall toward a that mass there is a transfer of energy from potential to kinetic. The initial potential energy of the particle is given by:
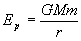 .....(18)
.....(18)
Where G = gravitational constant
M = mass of the major body
m = mass of the particle
r = distance between the two bodies
The final kinetic energy of the particle at the end of its fall will be:
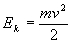 ....(19)
....(19)
Where v = final velocity of the particle.
If there is no other transfers of energy the initial potential energy must be equal to the final kinetic energy.
Therefore:
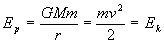
or
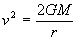 .....(20)
.....(20)
Spacial Effects
If we consider equation (12) we see:
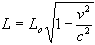 ...(12 from Special Relativity)
...(12 from Special Relativity)
Substituting for v2 gives:
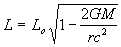 .....(21)
.....(21)
Therefore space is contracted within a gravitational field.
Temporal Effects
Similarly, if we consider equation (13) we see
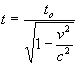 ...(13 from Special Relativity)
...(13 from Special Relativity)
Substituting for v2 gives:
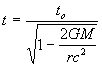 .....(22)
.....(22)
So we see that time is dilated within a gravitational field.
Frequency Effects
If we consider equation (14) we see:
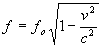 ...(14 from Special Relativity)
...(14 from Special Relativity)
Substituting for v2 gives:
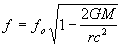 .....(23)
.....(23)
So we see that ligh within a gravitational field will also experience a Red Shift.
Mass Effects
If we consider equation (15) we see:
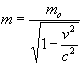 ...(15 from Special Relativity)
...(15 from Special Relativity)
Substituting for v2 gives:
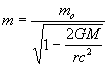 .....(24)
.....(24)
Thus, when the mass of an object is measered within a gravitational field it will seem greater than when measured in space free of gravitational fields.
Light Speed
From wave theory we note:
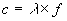 .....(25)
.....(25)
where c = speed of light
f = frequency
lamda = wave length.
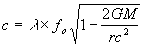
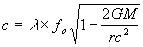
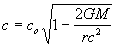 ...(26)
...(26)
This can be expanded into a series, similar to equation (16), whose first approximation is:
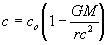 ...(27)
...(27)
Therefore the speed of light is slower inside a gravitational field.
Bending of Light
This should result in a measurable bending effect as light passes into and out of a gravitational field. Consider a wave of light.
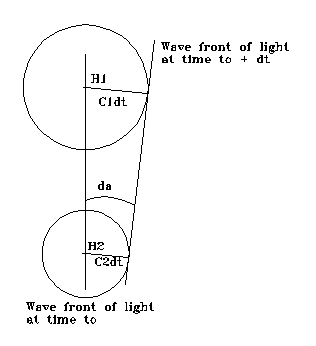
If we look at the wave front of a ray of light we note that the speed of light will vary across the length of the wave as indicated in equation (27). Thus the wave front will be deflected by an angle da in a time dt.
The angle of deflection in the distance C x dt is given by:
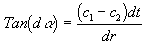
As da -> 0 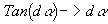
And : 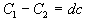
therefore: 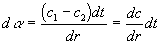 and the unit length
and the unit length 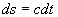
The deflection per unit length is found by dividing da by C.
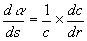 ...(28)
...(28)
Now from equation (27) we get:
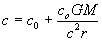
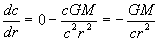
therefore:
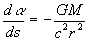 ...(29)
...(29)
Now the total deflection is given by the integral along the total path the light travels of the deflection angles da.
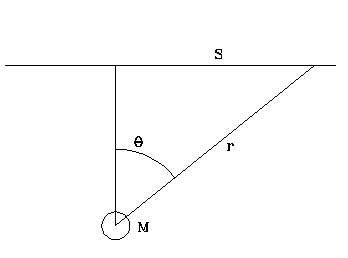
Now
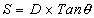
where D = distance of closest approach to the mass M
therefore 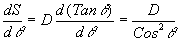
Therefore
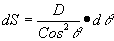 ....(30)
....(30)
Now:
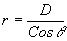 ....(31)
....(31)
Therefore:
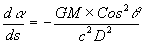
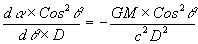
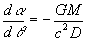
The total angle of deflection of the light ray is given by:
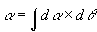 ...(32)
...(32)
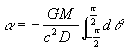
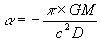 ...(33)
...(33)
where r = distance from the centre of the body.
G = Gravitational constant
M = mass of the body.
c = speed of light.
So we should be able to detect a bending of a ray of light caused by the gravitational field of a massive object. The only object in our solar system which produces a strong enough gravitational field to measure such a deflection is the sun. In this case:
D = 6.96 x 108 m (the radius of the sun).
G = 6.670 x 10-11 m kg-1 s-1
M = 1.99 x 1030 kg.
c = 3.0 x 108 m s-1.
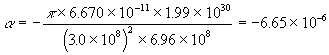 Radians
Radians
Or
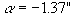 of arc
of arc
Einstein's Field Equation
Einstein quickly realised that these relationships reflected a distortion of space and time and that this distortion could be represented as a "curviture" in the space-time domain. To truely explore the relationships involved required an examination of the relationships between adjacent points in space-time. From geometry it is known that the distance between two points in three dimensions can be calculated knowing that:
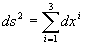 .....(34)
.....(34)
By extrapolation, it can be shown that for an arbitary number of dimensions this equation becomes:
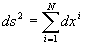 ......(35)
......(35)
In polar co-ordinates:
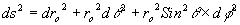
Extending this to 4 dimensions gives:
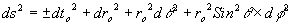 ......(36)
......(36)
At this stage the sign of the change in time is not yet determined. If the motion of a test particle is purely radial the angular terms in this equation can be ignored. Thus:
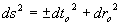 ........(37)
........(37)
Now from equation (21):
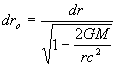 Or
Or 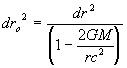
And from equation (22):
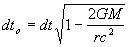 Or
Or 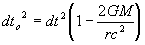
So equation (37) becomes:
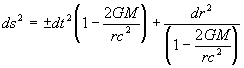 ....(38)
....(38)
Or in its more general form:
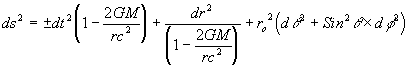 ....(39)
....(39)
The only thing remaining is to determine the sign of the time variable. We note that as r increases the unit of time t decreases with respect to the time measured by universal observer at a remote location and as r decreases the unit of time t increases with respect to the time measured by universal observer at a remote location. Therefore dt must always have the opposite sign to dr. Thus equation (39) becomes:
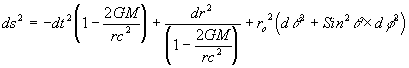 ....(40)
....(40)
Black Holes
Close examination of equation (40) shows that the metric for ds2 has problems at two conditions:
- When:
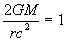
Or when:
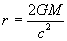
- When r = 0
In fact, if we consider equation (26) 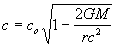 carefully we note that when
carefully we note that when 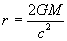 that c (the speed of light) = 0. Thus, light can not escape from the surface of such a body. For this reason they are refered to as "Black Holes". This critical radius is refered to as the "Event Horizon", for the simple reason that an observer outside the event horizon could not see (or measure) anything which takes place beyond this point.
that c (the speed of light) = 0. Thus, light can not escape from the surface of such a body. For this reason they are refered to as "Black Holes". This critical radius is refered to as the "Event Horizon", for the simple reason that an observer outside the event horizon could not see (or measure) anything which takes place beyond this point.
At r = 0, inside the event horizon, is the point called the "singularity". This is a mathematical term which indicates that a function tends toward infinity. In this case, the space-time functions tend toward infinity. Space becomes infinately contracted, while time becomes infinately dilated.
If all the mass of a body is compressed inside the event horizon radius, light will not escape from the surface of this body. For the sun this radius is approximately 2.95 x 103 m. Presumably, all the matter within the body will then continue to fall into the singularity, but there is no way of really knowing this from the outside of such an object.
Matrix Form of the Field Equations
Returning to equation (40), this type of equation can be better represented in matrix form. After some time, Einstein did manage to produce a mathematical equation to describe the behaviour of time and space in the presence of objects in matrix form. The equation is:
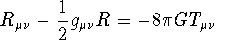 ...(41)
...(41)
where the terms, 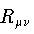 (Riemann's power tensor),
(Riemann's power tensor), 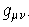 and
and  are all matricies.
are all matricies.
The format of the equation is that matter "tells" space-time how to distort (curve) while the curviture of space-time "tells" matter how to move.