collected by Lambert Dolphin
Ongoing Discussion: Barry Setterfield's web site now features discussion sections where the following issues, and many more, are currently being posted and discussed. You may email Barry at barry4light2@yahoo.com. (March 9, 2003)
Australian astronomer Barry Setterfield suggests that all "constants" which carry units of "per second" have been decreasing since the beginning of the universe. Constants with dimensions of "seconds" have been increasing inversely. This is born out with some degree of statistical confidence by studying the available measurements of all the constants over time. The case for the velocity of light decreasing is better established than changes in any other constants because more data over longer time periods is available for c.
Measurements on constants of physics which do not carry dimensions of time (seconds or 1/seconds; or powers thereof) are found to be truly fixed and invariant. The variability of one set of constants does not lead to an unstable universe, nor to readily observable happenings in the physical world. The principal consequence is a decreasing run rate for atomic clocks as compared to dynamical clocks. The latter clocks depend on gravity and Newton's Laws of Motion.
In the first thorough statistical study of all the available data on the velocity of light in recent decades, presented in Barry Setterfield and Trevor Norman's 1987 report The Atomic Constants, Light, and Time, the authors also analyzed (in addition to values of c), measurements of the charge on the electron, e, the specific charge, e/mc, the Rydberg constant, R, the gyromagnetic ratio, the quantum Hall resistance, h/e2, 2e/h, and h/e, various radioactive decay constants, and Newton's gravitational constant G.
Three of these Norman and Setterfield quantities found to be truly fixed constants, namely e, R, and G. These constants are either independent of time or independent of atomic processes. The other five quantities, which are related to atomic phenomena and which involve time in their units of measurement, were found to trend, with the exception of the quantum Hall resistance.
Montgomery and Dolphin re-analyzed these data, carefully excluding outliers. Their results differed from Norman and Setterfield's only for the Rydberg constant where Montgomery and Dolphin obtained rejection of constancy at the 95% confidence level for the run test (but not the MSSD). The available measurements of radioactive decay constants, they found, do not have enough precision to be useful. Montgomery's latest work answers his critics and used statistical weighting.
Norman and Setterfield also believe that photon energy, (hf), remains constant over time even as c varies. This forces the value of (hc) to be constant in agreement with astronomical observations. What is measured astronomically are light wavelengths, not frequency. The consequence of this is that h must vary inversely with c and therefore the trend in the constants containing h are restricted as to their direction. The Fine Structure constant is invariant. An increasing value of h over time affects such things as the Heisenberg Uncertainty Principle.
Montgomery and Dolphin calculated the least-squares straight line for all the c-related constants and found no violation of this restriction. In all cases the trends in "h constants" are in the appropriate direction. In addition, a least squares line was plotted for c, the gyromagnetic ratio, q/mc, and h/e for the years 1945-80. The slopes continued to remain statistically significant, and in the appropriate direction. Furthermore the percentage rate of change varied by only one order of magnitude---very close, considering how small some of the cells are. By contrast, the t test results on the slopes of the other three constants (e, R, and G) were not statistically significant. See Is The Velocity of Light a Constant in Time?
To summarize: The Bohr Magnetron, gas constant R(0), Avogadro's number, N(0), Zeeman Displacement/gauss, the Schrodinger constant (fixed nucleus), Compton wavelengths, the Fine Structure Constant, deBroglie wavelengths, the Faraday and the Volt (hf/2e) all can be shown to be c-independent. The gravitational constant G, actually more properly speaking Gm, appears to be a fixed constant.
The velocity of electromagnetic waves has its present value of 299,792.458 km/sec, only in vacuum. When light enters a denser medium, such as glass or water the velocity in the medium drops immediately by a factor of one over the index of refraction (n) of the medium. For practical purposes, the index of refraction is equal to the square root of the dielectric constant of the medium---which is the real part of the dielectric permittivity of the medium. Materials other than vacuum are lossy, causing electromagnetic waves to undergo dispersion as well a change in wavelength in the medium.
For example, the dielectric constant of water at radio wavelengths is about 81, so the velocity of radio waves in water is 299,792.458 / 9 or 33,310.273 km/sec. In the visible light band, n is about 1.3 for water, giving a velocity of 225,407.863 km/sec for visible light rays.
Actually the velocity of light is a scaling constant, or metric, which appears in James Clerk Maxwell's equations for the propagation of electromagnetic waves in any medium. The velocity of light is dependent not only on the dielectric permittivity, e,---in free space designated as e(0); but also on the magnetic permeability of a medium, m,---which for free space is designated as m(0).
The propagation velocity for electromagnetic waves, c, is related to e and m according to the following equation,
1/c2 = m0e0
c = 1/[m0e0]1/2
After discussing both options as to whether it was m or e that might be varying, Setterfield and Norman originally suggested that the permittivity of free space has not changed with time according to the best available measurements. It was probably the permeability which was changing---possibly inversely proportional to c squared. The permeability of space was apparently related in some way to the stretching out of free space at the time of creation (Genesis 1:6-8, Psalm 104:2). It might be possible, therefore, that when God stretched out the "firmament of the heavens"---on the second day of creation week---that the value of (m) had its lowest value and had since increased.
According to this earlier hypothesis, sometime after creation the heavens apparently "relaxed" from their initial stretched-out condition, much as one would let air out of a filled balloon. If the universe had its maximum diameter at the end of creation week and had since shrunk somewhat, then the Big Bang theory of an expanding universe is incorrect. The shrinkage of free space would then account for the observed slowing down of the velocity of light. The red-shift would not be a measure of actual radial velocities of the galaxies receding from one another, but instead would be due entirely to a decrease in the value of c since creation. An initial value of c some 11 million times greater than the present value of c was suggested.
William Sumner's recent paper (see abstract) proposes a cosmology in which permittivity rather than permeability is the variable. Glenn R. Morton discusses both possibilities and their consequences in his useful CRSQ paper, Changing Constants and the Cosmos. (Creation Research Society Quarterly, vol. 27 no. 2, September 1990)---available from Creation Research Society
More recently Barry Setterfield (private communication) has suggested that he now believes that both e and m are varying. This follows from the fact that in the isotropic, non-dispersive medium of space, equal energy is carried by the Electric and Magnetic vector components of the electromagnetic wave, and the ratio of E/H is invariant with any change in c. Therefore both e and m have been changing over time since creation. In the revised view, the apparent decrease in c since creation could be due to a step input of Zero Point Energy (ZPE) being fed into the universe from "outside"---as a function of time, beginning just after the heavens were stretched out to the maximum diameter on Day Two of creation. The diameter of the universe has been fixed (static) ever since, so one must look for another explanation of the Red Shift than the old model of an expanding universe. This view does not rule out possible subsequent decreases in the ZPE input from the vacuum which might be associated with such catastrophes in nature as the fall of the angels, the curse on the earth at the fall of man, and the flood of Noah catastrophe. Such changes would result in the universe being more degenerative now than it was at the end of creation week.
Some additional published information by Setterfield is available by mail from Australia (Reference 1), but most Setterfield's later work is awaiting final peer review for journal publication as of this writing.
From Maxwell's electromagnetic theory, we can also calculate what is known as the "impedance of free space" (commonly used in antenna design). The present value is 377 ohms, and the formula is,
Z = [m0/e0]1/2
n = [e/m][E/H]
As noted above, the impedance of free space tells us how radio waves, or photons of light, will travel through space. Z also gives us the ratio of the electric field vector, E, to the magnetic field vector, H, in free space. Z is also invariant with changes in c. The refractive index of any medium---whether empty space or other material, n, measures the property of a glass lens to bend a beam of light for example. If c were found to be decreasing over the history of the universe it follows that optical path lengths everywhere in the universe have been changing since creation. This result has a number of consequences for astronomy---the true size and the age of the universe would be greatly affected for instance. It has been argued that no change in light spectra from distant stars has ever been observed and hence c could not have changed. As will be seen below, what is measured in light spectra is always wavelength not frequency; light wavelengths stay constant with varying c. Constants such as alpha, the fine-structure constant, (and so on) are invariant if c changes.
The energy carried by an electromagnetic propagating wave is contained in both the oscillating magnetic field and the oscillating electric field. The total energy flux is known as Poynting's Vector, S. S is equal to c times the cross product of the E and H vectors. Energy is conserved in propagating waves---at least no one wishes to throw out such an important principle at least as a first approach.
Assuming energy is conserved under conditions of decreasing c the following must be true:
The energy of a photon can be calculated from Einstein's famous equation relating mass and energy. If we use this formula, it is easy to see that the photon has "apparent mass" as is often noted. Photon energy is also known to be equal to hf, where h is Planck's constant and f is the frequency of the emitted light of the photon. The energy of a photon can also be expressed in terms of wavelength, lambda, rather than frequency,
Energy, E = mc2
E = hv = hc/l
if c is non-constant then hc = constant and h ~ 1/c.
If c is not a fixed constant, Planck's "constant" should vary with time, that is inversely proportional to c. (That this is so experimentally is borne out with reasonable statistical confidence levels by data given in the Setterfield and Norman 1987 report and also by Montgomery and Dolphin in their Galilean Electrodynamics paper).
In their original theory Setterfield and Norman believed that the wavelength of radiation, at the time a radio-wave or light photon is emitted, is invariant for constant energy. However, once a radio-wave leaves the source, or a photon departs from its parent atom, energy and momentum are apparently both conserved. Also the product (hc) is a true constant which does not vary with time.
In their 1987 report, Setterfield and Norman show that the deBroglie wavelengths for moving particles and the Compton wavelength are c-independent. The energy of an orbiting electron, the fine-structure constant, and the Rydberg constant are also shown to be c-independent and thus truly constant with time. The gyro-magnetic ratio, g = e/ 2mc, is found to vary inversely proportionally to c.
Setterfield and Norman originally claimed that the wavelength of light emitted from atoms, (for instance, the atoms on a distant star), was independent of any changes in c. However, the relative energy of the emitted light wave is inversely proportional to c, and if c decreases while the light wave is on its journey, its energy and its momentum must be conserved in flight. The intensity of the light, related to the wave amplitude, increases proportionally to c. Thus there should be proportionally less dimming of light from distant stars. In order for light to maintain energy conservation in flight, as c decays, the frequency of the emitted light must decrease inversely proportionally to c. The relaxation of free space, causing the observed c-decay, and increasing optical path length, occurs everywhere in the universe at the same time.
A new explanation of the (quantized) red-shift involving a static (non-expanding) universe is the subject of a paper now in preparation by Barry Setterfield.
Setterfield's early attempts to explain the red shift as caused by the decrease in light velocity over time were not satisfactory. Several other researchers also tried to explain the red-shift as a Doppler-like effect. Setterfield revised his model in 1993 along the following lines:
Barry now assumes that energy flux from our sun or from distant stars is constant over time. (Energy flux is due to atomic processes and is the amount of energy radiated from the surface of a star per square centimeter per second). Setterfield also now proposes that when the velocity of light was (say) ten times higher than now, then 10 times as many photons per second (in dynamical time) were emitted from each square centimeter of surface. Each photon would however carry only one tenth as much energy, conserving the total energy flux. Setterfield says, "This approach has a dramatic effect. When light-speed c was 10 times higher, a star would emit 10 photons in one second compared with one now. This ten-photon stream then comprised part of a light beam of photons spaced 1/10th of a second apart. In transit, that light beam progressively slowed until it arrived at the earth with today's c value. This speed is only 1/10th of its original speed, so that the 10 photons arrive at one second intervals. The source appears to emit photons at today's rate of 1 per second. However, the photon's wavelength is red-shifted, since the energy per photon was lower when it was emitted."
Setterfield continues, "This red-shift of light from distant galaxies is a well-known astronomical effect. The further away a galaxy is from us, the further down into the red end of the rainbow spectrum is its light shifted. It has been assumed that this is like a Doppler effect: when a train blowing its whistle, passes an observer on a station, the pitch of the whistle drops. Similarly light from galaxies was thought to be red-shifted because the galaxies were racing away from us. Instead, the total red-shift effect seems due to c variation alone."
"When this scenario is followed through in mathematical detail an amazing fact emerges. The light from distant objects is not only red-shifted: this red-shift goes in jumps, or is 'quantized' to use the exact terminology. For the last 10 years, William Tifft, an astronomer at (an) Arizona Observatory USA, has been pointing this out. His most recent paper on the matter gives red-shift quantum values from observation that are almost exactly (those) obtained from c-variation theory. Furthermore, a theoretical value can be derived for the Hubble constant, H. As a consequence, we now know from the red-shift how far away a galaxy was, and the value of c at the time the light was emitted. We can therefore find the value of c right out to the limits of the universe...Shortly after the origin of the universe, the red-shift of light from distant astronomical objects was about 11 million times faster than now. At the time of the Creation of the Universe, then, this high value of c meant the atomic clock ticked off 11 million years in one orbital year. This is why everything is so old when measured by the atomic clock." (Ref. 1)
Setterfield's original reasoning concerning the relationships between energy and mass were somewhat as follows: The energy, E, associated with a mass, m, is E = m c2, as stated earlier. This means that the mass of an object would seem to vary as 1/c2. At first this seems preposterous. However Setterfield noted that "m" in the above equation is the atomic (or rest) mass of a particle, not the mass of the particle if the particle were weighed on a gravity type scale.
The factor for converting mass from atomic mass to dynamical mass is precisely c squared. As c decreases no change in the mass of objects is observed in our ordinary experience because we observe the gravitational and inertial properties of mass in dynamical, not atomic time. To better understand the difference between atomic rest mass, and mass weighed in the world of our daily experience, consider Newton's Law of Gravity.
As far as gravity is concerned, the gravitational force, F, between objects of mass m and M is given by Newton's formula,
F = GMm/r2
where G is the universal gravitational constant and r is the distance between the objects. Space has built-in gravitational properties similar to its electrical properties mentioned above. This gives rise to the so-called "Schwartschild metric for free space," which also is related to the stretched-outness of free space. In this way of viewing things macroscopic mass measured by gravity is atomic rest mass multiplied by the so-called gravitational permeability of free space, corresponding to electromagnetic permeability in Maxwell's equations. (See Ref. 2)
Incidentally, the accepted value of G is 6.67259 x 10-11) and the units are: meters3 kg-1) sec-2. Clues as to which units should be fixed and which are invariant, as noted in the first paragraph above, are "constants" containing "seconds" or "1/seconds" or powers thereof. If Gm is invariant, then Setterfield's latest work implies that G itself varies inversely with c to the fourth power.
More recently Setterfield has attempted to relate a decreasing velocity of light with astronomer William Tifft's discovery that red-shifted light from the galaxies appears to be quantized. Setterfield also notes (as does Hal Putoff) that in classical atomic theory electrons circling the nucleus are accelerated particles and ought to radiate energy, but apparently they don't--according to the tacit assumptions of modern physics. Setterfield suggests that energy is actually being fed into every atom in the universe from the vacuum at precisely the rate electrons are dissipating this energy. The calculated total amount of this energy input is enormous, of the order of 1.071 x 10117 kilowatts per square meter. (Some have physicist have claimed that the latent energy resident in the vacuum is infinite, but Setterfield is content to be conservative, he says!) 10117 is of course a very large number in any case. [The total number of atoms in the universe is only ~ 1066, the total number of particles in the universe is only ~ 1080, the age of the universe is only about ~ 1017 seconds. And any event with a probability of less than 1 part in 1050 is considered "absurd."]
After the initial creation of space, time and matter, and the initial stretching out of the universe to its maximum (present) diameter, the above-mentioned energy input from the vacuum commenced as a step impulse and has continued at the same rate ever since. [Assuming no subsequent disruptions from "outside"]. This energy input has raised the energy density of the vacuum per unit volume over time and means the creation and annihilation of more virtual particles as time moves forward. Photons are absorbed and reradiated more frequently as this takes place, hence the velocity of light decreases with time. All this is another way of saying that the properties of the vacuum as measured by mu and e have changed as a function of time since the creation event.
Furthermore as the velocity of light drops with time, atoms in the vicinity continue for a certain time period radiating photons of the same wavelengths for a season, and then abruptly every energy level drops by one quantum number. According to Setterfield's estimates, the velocity of light must decrease by the incremental value of 331 km/sec for one quantum jump of wavelength in photons radiated from atoms to occur. (There have been somewhere around 500,000 total quantum jumps since the universe began, he estimates). The last jump occurred about 2800 B.C.
This, then, in brief provides a new explanation for the red-shift and the quantization of red-shifted light from the galaxies which has been documented by Wm. Tifft and others in recent years.
Setterfield now suggests that the product of G and m is a fixed constant, rather than G itself. When one attempts to measure G in the laboratory (this is now done with great precision) he claims that we actually measure Gm. In Setterfield's latest work, rest mass m varies inversely as c squared except at the quantum jumps when m is inversely proportional to c to the fourth power. In such a model energy is not conserved at the jumps, because more energy is being fed into the universe from the vacuum. Energy conservation holds between the quantum jump intervals. Since Setterfield's latest work has not been published, the best source of related information is his last published report and video, (Reference 1). Three charts from that report are accessible from this web page.
Setterfield's paper on this subject is in final journal review as of this writing. Overview of theory, Atomic Behaviour, Light and The Red-Shift.
Consider the Bohr atom for purposes of illustration. The centripetal force pushing electrons away from the nucleus is exactly balanced by the electrostatic (Coulomb) force between electron and nucleus.
F = e2/4pe0r2 = mv2/r
v = e2/e02nh
hence v varies as c
v is the orbital velocity of the electron, e is its charge, h is Planck's constant, r is the orbital radius of the electron, F the force and m the rest mass of the electron.
From this simplistic approach, if c is decreasing with time, then Planck's constant is increasing, and orbital velocities were faster in the past---thus the "run rate" of the atomic clock was faster in the past. Of course Setterfield has worked out the mathematics for more sophisticated quantum mechanical models of the atom, and also shown that his conclusions do not conflict with either General or Special Relativity Theories.
If the above equation is solved for rest mass m, then m is proportional to Planck's constant squared. That makes m inversely proportional to c squared in the Setterfield model.
Additional notes from the 1987 Setterfield and Norman report: "For energy to be conserved in atomic orbits, the electron kinetic energy must be independent of c and obey the standard equation:
E(k) = mv2 / 2 = [Z e2] / (8 pi epsilon(0) a] = invariant with changes in c.
The term e2 / e(0) is also c independent as are atomic and dynamical orbit radii. Thus, the atomic orbit radius, a, is invariant with changes in c.
However for atomic particles, the particles velocities, v, are proportional to c.
Now from Bohr's first postulate (the Bohr Model is used for simplicity throughout as it gives correct results to a first approximation) comes the relation,
mva = nh / 2 pi
where h is Planck's constant. Thus h varies as 1/c..."
"The expression for the energy of a given electron orbit, n, is,
E(n) = 2 pi2 e4 m / [h2 n2]
which is independent of c. With orbit energies unaffected by c decay, electron sharing between two atomic orbits results in the 'resonance energy' that forms the covalent bond being c independent. A similar argument also applies to the dative bond between coordinate covalent compounds. Since the electronic charge is taken as constant, the ionic or electrovalent bond strengths are not dependent on c.
Related to orbit energy is the Rydberg constant R.
R = 2 pi2 e4 m / [(c h3]
which is invariant with changes in c, as the mutually variable quantities cancel...
The Fine Structure constant, alpha, appears in combination with the Rydberg constant in defining some other quantities...
the fine structure constant,
alpha = 2 p2 / (hc),
which is invariant with c." (End of excerpt from 1987 Setterfield and Norman report)
In their 1987 essay, Setterfield and Norman suggested that radioactive decay processes were proportional to c. (There are various mechanisms for radioactive emission processes, the equations for each model all involve c or h in the same general fashion).
The following notes are also taken from the Setterfield and Norman 1987 report: "...the velocity, v, at which nucleons move in their orbitals seems to be proportional to c. As atomic radii are c independent, and if the radius of the nucleus is r, then the alpha particle escape frequency lambda* (the decay constant) as defined by Gladstone and Von Buttlar is given as,
lambda* = P v / r
where P is the probability of escape by the tunneling process. Since P is a function of energy, which, from the above approach is c independent, then lambda* varies in proportion to c.
For beta decay processes, Von Buttlar defines the decay constant as,
lambda* = G f = m c2 g2 |M|2 f / [p2 h]
where f is a function of the maximum energy of emission and atomic number Z, both c independent. M, the nuclear matrix element dependent upon energy, is unchanged by c, as is the constant g. Planck's constant is h, so for beta decay, lambda* varies in proportion to c. An alternative formulation by Burcham leads to the same result.
For electron capture, the relevant equation from Burcham is lambda* = K2 |M|5 f / [2 p2]
where f is here a function of the fine structure constant, the atomic number Z, and total energy, all c independent. M is as above. K2 is defined by Burcham as,
K2 = g2 m2 c4 / [h / 2 p]
With g independent of c, this results in K2 proportional to c, so that for electron capture lambda* varies in proportion to c. This approach thus gives lambda* proportional to c for all radioactive decay [processes]...
The beta decay coupling constant, g, used above, also called the Fermi interaction constant, bears a value of 1.4 x 10-49 [erg-cm] [^ 3]. Conservation laws therefore require it to be invariant with changes in c. The weak coupling constant, g , is a dimensionless number that includes g. Wesson defines g(w) = {[g m2 c / (h / 2 p)3]}2, where m is the pion mass...this equation also leaves g(w) as invariant with changes in c. This is demonstrable in practice since any variation in gw would result in a discrepancy between the radiometric ages for alpha and beta decay processes. That is not usually observed. The fact that g(w) is also dimensionless hinted that it should be independent of c for reasons that become apparent shortly. Similar theoretical and experimental evidence also shows that the strong coupling constant, g has been invariant over cosmic time. Indeed, the experimental limits that preclude variation in all three coupling constants also place comparable limits on any variation in e or vice versa. The indication is, therefore, that they have remained constant on a universal timescale. The nuclear g-factor for the proton, g(p) , also proves invariant from astrophysical observation. Generally, therefore, the dimensionless coupling constants may be taken as invariant with changing c." (End of excerpt)
Radioactive decay rates have been experimentally measured only in this century. The available data has been statistically examined by Trevor Norman and also by Alan Montgomery (both very competent statisticians) but without conclusive results because of the paucity of data.
Was the energy released by radioactive decay processes faster in the past when c was higher? Setterfield says, "...there is an elegant answer to this question. Light is an electromagnetic phenomenon whereby energy is transported. In this scenario, the fundamental entity is not the energy as such, but rather the rate of flow of that energy at its point of emission. What is proposed here for variable 'c' is that the amount of energy being emitted per unit time from each atom, and from all atomic processes, is invariant. In other words the energy flux is conserved in all circumstances with c variation. This solves our difficulty.
"Under these new conditions the radio-active decay rate is indeed proportional to 'c'. However, the amount of energy that flows per orbital second from the process is invariant with changes in 'c'. In other words, despite higher 'c' causing higher decay rates in the past, this was no more dangerous then than today's rates are, since the energy flux is the same. This occurs because each emitted photon has lower energy. As the reactions powering the sun and stars have a similar process, a potential problem there disappears as well.
"What is being proposed is essentially the same as the water in a pipe analogy. Assume that the pipe has a highly variable cross-section over its length. As a result, the stream of water moves with varying velocity down the pipe. But no matter how fast or slow the stream is moving, the same quantity of water flows per unit time through all cross-sections of the pipe. Similarly, the emitted energy flux from atomic processes is conserved for varying c values. Under these conditions, when the equations are reworked all of the previously mentioned terrestrial and astronomical observations are still upheld. Indeed, the synchronous variations of the same constants still occur." (From Ref. 1)
What is noticeably different in a universe where c is decreasing? Macroscopically not very much, Setterfield and Norman have claimed. Gravity is not affected, nor Newton's Laws of motion, nor most processes of chemistry or physics. The stability of the universe in the usual cosmological equations is unaffected, although one or more very different cosmological scenarios for the history of the universe can be developed as shown in the accompanying abstracts by Troitskii, Sumner, and Hsu and Hsu. Of course these new models differ from the currently prevailing Big Bang scenario in many significant ways.
Because wavelength of light (not frequency) is measured, we would not detect changing c by measurements of absolute wavelengths of light from distant stars over time, or by changes in spectral line splitting and so on.
The main effect of changing c concerns time scales measured inside the atom---on the atomic scale---as opposed to macroscopic events as measured outside the atom. Put another way, the run rate of the atomic clock would slow with respect to dynamical time (as measured by the motion of sun, moon, and stars.)
Prof. of Biology Dean Kenyon of San Francisco State University has suggested (private communication) that if c were higher in the past some biological processes could have been faster or more efficient in the past. Nerve impulses are of course not completely electrical in nature because of the ion-transfer processes at neuron synapses for instance.
Notes from Setterfield:
SEVEN RELEVANT BASIC FEATURES OF THE NEW THEORY:
1. Photon energies are proportional to [l / c2)].
2. Photon fluxes from emitters are directly proportional to c.
3. Photons travel at the speed of c.
4. From 1 to 3 this means that the total energy flux from any emitter is invariant with decreasing c, that is, [ 1 / c2 x c x c ]. This includes stars and the radioactive decay of elements etc.
5. Atomic particles will travel at a rate proportional to c.
6. There is an additional quantization of atomic phenomena brought about by a full quantum (+/-) of energy available to the atom. This occurs every time there is a change in light-speed by (+/-) 331 times its present value.
7. A harmonization of the situation with regards to both atomic and macroscopic masses results from the new theory, and a quantization factor is involved.
RESULTS FROM THOSE SEVEN FEATURES:
A). From 2, as photosynthesis depends upon the number of photons received, it inevitably means that photosynthetic processes were more efficient with higher c values. This leads to the conclusions stated originally.
B). As radiation rates are proportional to c from 2, it inevitably follows that magma pools, e.g., on the moon, will cool more quickly. Note that A and B are built-in features of the theory that need no other maths or physics.
C). From 6 and 7, the coefficient of diffusion will vary up to 331 times its current value within a full quantum interval. In other words there is an upper maximum to diffusion efficiencies. Otherwise the original conclusions still stand.
D). In a similar way to C, and following on from 6 and 7, the coefficient of viscosity will vary down to 1/331 times it current value within the full quantum interval. This implies a lower minimum value for viscosities. Within that constraint, the original conclusions hold.
E). In a way similar to C and D, and again resulting from 6 and 7, critical velocities for laminar flow will vary up to 331 times that pertaining now, within the full quantum interval. The original conclusions then hold within that constraint.
F). As the cyclic time for each quantum interval was extremely short initially, it follows that it is appropriate to use an average value in C, D, and E, instead of the maximum: that is, about 166. As c tapered down to its present value, a long time has been spent on the lower portion of a quantum change with near-minimum values for C, and E, and near maximum values for D. These facts result in the effects originally elucidated.
(Additional notes in this paragraph supplied by Barry Setterfield, 6th November, 1995).
In their most recent publication Setterfield and Norman provide a curve with their proposed rate of decrease in c with both dynamical and atomic time scales shown. A scanned copy of their curve is available at the end of this paper under Reference 1. Their most recent published formula for the rate of decrease in c is,
Conversion from atomic time to dynamic time for
atomic dates
greater than 63 million years (1005 B.C. in dynamical time):
D - (63 million) = 1905 t2
where D is Dynamical time and t is atomic time.
when t is obtained from this equation, add 3005 years to get actual
year B.C.
Time after creation, in orbital years is approximately,
D = 1499 t2 (Setterfield Ref. 1)
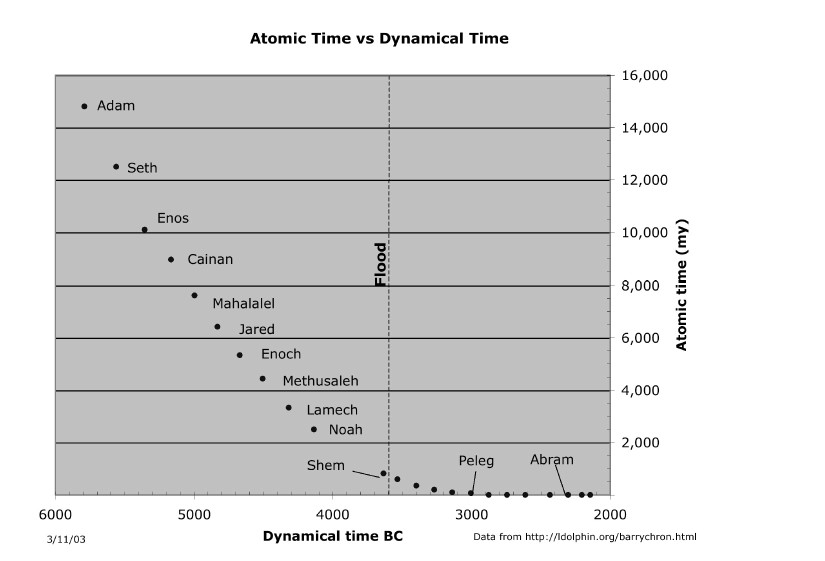
The initial value of c is believed to have been greater than the present value by a factor of 11 million times. In the past 4000 years or so, Setterfield believes the velocity of light has decreased exponentially to nearly zero at the present time. In order to get a grasp on how c may have changed in the time period from 2550 B.C. to the present, Setterfield spent 9 months collecting some 1228 published radiometric dates which could be correlated with known actual historical dates from ancient history or archaeology. For instance, cedar from the great pyramid of Giza has been radio-carbon dated and the pyramid was believed to have been built in 2650 B.C. The two dates do not coincidence even when a corrected radio-carbon dating curve is used. A plotted curve of these 1228 data points by Setterfield showing how c may have varied since 2550 B.C. is accessible below under Reference 1. Setterfield has superposed an damped (oscillatory) exponential tail as a best-fit curve to the plot of the data.
Setterfield says, "Unlike our first presentation [i.e., the 1987 report] which has been shown to have no red-shift, z, with CDK, [CDK = "c decay"] this revised approach indicates that the red-shift of light from distant galaxies is certainly a CDK effect. Indeed, the derivation gives red-shifts that are quantized in jumps of 2.732 km/s. This figure and its 3rd and 5th multiples give inferred velocities that have been observed by Tifft, et al (Astrophys. J., Vol. 382, pp.396-415, Dec. 1, 1991).
"Furthermore, there is no red-shift from CDK for astronomical objects closer than 126,000 Light Years. On this basis, then, these z values provide CDK data out to the limits of the cosmos. The form of CDK is clearly discernible...These data reveal a clear decay pattern. A steep square-law drop bottomed out near 2800 BC. Because of the overshoot, c then underwent an oscillation about its final value with the last maximum about 1200 AD. The measured value of c has dropped since then...Conversion from atomic eras to fairly exact dates in actual orbital time is thus a simple process...The reason for CDK, and aberrant atomic clock Behaviour, seems to lie in the reaction of the 'fabric' of space to the massive energy input at the time of creation. The initial value of c was about 11 million times its current speed. Troitskii's less formal analysis placed it at roughly 10 billion times c now." (Ref. 1)
If the age of the universe is 15 billion years in atomic time, then this number is equivalent to a historical (dynamical time) date of about 6000 B.C.
It should be obvious that there are major problems remaining to be addressed if such alleged rates of change and the underlying causes are to be explained, defended, and analyzed properly in peer-reviewed journals. The above remarks are both abbreviated and tentative to say the least.
In his last published paper A Determination and Analysis of Appropriate Values of the Speed Of Light ... Alan Montgomery gives a curve to fit the available data as follows:
c ( t ) = 299,792 + .031 x [ ( 1967.5 - t )2].
Montgomery says this "is a suitable regression model for the velocity of light values in the last 250 years."
Notes on a Static Universe:Incredibly, an expanding universe does imply an expanding earth on most cosmological models that follow Einstein and or Friedmann. As space expands, so does everything in it. This is why, if the redshift signified cosmological expansion even the very atoms making up the matter in the universe would also have to expand. There would be no sign of this in rock crystal lattices etc since everything was expanding uniformly as was the space between them. This expansion occurred at the Creation of the Cosmos as the verses you listed have shown.
It is commonly thought that the progressive redshift of light from distant galaxies is evidence that this universal expansion is still continuing. However, W. Q. Sumner in Astrophysical Journal 429:491-498, 10 July 1994, pointed out a problem. The maths indeed show that atoms partake in such expansion, and so does the wavelength of light in transit through space. This "stretching" of the wavelengths of light in transit will cause it to become redder. It is commonly assumed that this is the origin of the redshift of light from distant galaxies. But the effect on the atoms changes the wavelength of emitted light in the opposite direction. The overall result of the two effects is that an expanding cosmos will have light that is blue-shifted, not red-shifted as we see at present. The interim conclusion is that the cosmos cannot be expanding at the moment (it may be contracting).
Furthermore, as Arizona astronomer William Tifft and others have shown, the redshift of light from distant galaxies is quantized, or goes in "jumps". Now it is uniformly agreed that any universal expansion or contraction does not go in "jumps" but is smooth. Therefore expansion or contraction of the cosmos is not responsible for the quantization effect: it may come from light-emitting atoms. If this is so, cosmological expansion or contraction will smear-out any redshift quantization effects, as the emitted wavelengths get progressively "stretched" or "shrunk" in transit. The final conclusion is that the quantized redshift implies that the present cosmos must be static after initial expansion. [Narliker and Arp proved that a static matter-filled cosmos is stable against collapse in Astrophysical Journal 405:51-56 (1993)].
Therefore, as the heavens were expanded out to their maximum size, so were the earth, and the planets, and the stars. I assume that this happened before the close of Day 4, but I am guessing here. Following this expansion event, the cosmos remained static. (Barry Setterfield, September 25, 1998)
Question: What about the new evidence that the rate of expansion of the universe is accelerating as reported in recent science articles?
Comment from Barry Setterfield:The evidence that an accelerating expansion is occurring comes because distant objects are in fact further away than anticipated given a non-linear and steeply climbing red-shift/distance curve.
Originally, the redshift/distance relation was accepted as linear until objects were discovered with a redshift greater than 1. On the linear relation, this meant that the objects were receding with speeds greater than light, a no-no in relativity. So a relativistic correction was applied that makes the relationship start curving up steeply at great distances. This has the effect of making large redshift changes over short distances. Now it is found that these objects are indeed farther away than this curve predicts, so they have to drag in accelerating expansion to overcome the hassle.
The basic error is to accept the redshift as due to an expansion velocity. If the redshift is NOT a velocity of expansion, then these very distant objects are NOT traveling faster than light, so the relativistic correction is not needed. Given that point, it becomes apparent that if a linear redshift relation is maintained throughout the cosmos, then we get distances for these objects that do not need to be corrected. That is just what my current redshift paper does. (January 12, 1999)
Question: Regarding the recent research acknowledging the possibility that the speed of light has not always been constant, someone wrote to me: "By the way, there's a pretty easy way to demonstrate that the speed of light has been constant for about 160,000 years using Supernova 1987A."
Comment from Barry Setterfield: It has been stated on a number of occasions that Supernova 1987A in the Large Magellanic Cloud (LMC) has effectively demonstrated that the speed of light, c, is a constant. There are two phenomena associated with SN1987A that lead some to this erroneous conclusion. The first of these features was the exponential decay in the relevant part of the light-intensity curve. This gave sufficient evidence that it was powered by the release of energy from the radioactive decay of cobalt 56 whose half-life is well-known. The second feature was the enlarging rings of light from the explosion that illuminated the sheets of gas and dust some distance from the supernova. We know the approximate distance to the LMC (about 165,000 to 170,000 light years), and we know the angular distance of the ring from the supernova. It is a simple calculation to find how far the gas and dust sheets are from the supernova.
Consequently, we can calculate how long it should take light to get from the supernova to the sheets, and how long the peak intensity should take to pass.
The problem with the radioactive decay rate is that this would have been faster if the speed of light was higher. This would lead to a shorter half-life than the light-intensity curve revealed. For example, if c were 10 times its current value (c now), the half-life would be only 1/10th of what it is today, so the light-intensity curve should decay in 1/10th of the time it takes today. In a similar fashion, it might be expected that if c was 10c now at the supernova, the light should have illuminated the sheets and formed the rings in only 1/10th of the time at today's speed. Unfortunately, or so it seems, both the light intensity curve and the timing of the appearance of the rings (and their disappearance) are in accord with a value for c equal to c now. Therefore it is assumed that this is the proof needed that c has not changed since light was emitted from the LMC, some 170,000 light years away.
However, there is one factor that negates this conclusion for both these features of SN1987A. Let us accept, for the sake of illustration, that c WAS equal to 10c now at the LMC at the time of the explosion. Furthermore, according to the c decay (cDK) hypothesis, light-speed is the same at any instant right throughout the cosmos due to the properties of the physical vacuum. Therefore, light will always arrive at earth with the current value of c now. This means that in transit, light from the supernova has been slowing down. By the time it reaches the earth, it is only traveling at 1/10th of its speed at emission by SN1987A. As a consequence the rate at which we are receiving information from that light beam is now 1/10th of the rate at which it was emitted. In other words we are seeing this entire event in slow-motion. The light-intensity curve may have indeed decayed 10 times faster, and the light may indeed have reached the sheets 10 times sooner than expected on constant c. Our dilemma is that we cannot prove it for sure because of the slow-motion effect. At the same time this cannot be used to disprove the cDK hypothesis. As a consequence other physical evidence is needed to resolve the dilemma. This is done in the forthcoming paper where it is shown that the redshift of light from distant galaxies gives a value for c at the moment of emission.
By way of clarification, at NO time have I ever claimed the apparent superluminal expansion of quasar jets verify higher values of c in the past. The slow-motion effect discussed earlier rules that out absolutely. The standard solution to that problem is accepted here. The accepted distance of the sheets of matter from the supernova is also not in question. That is fixed by angular measurement. What IS affected by the slow motion effect is the apparent time it took for light to get to those sheets from the supernova, and the rate at which the light-rings on those sheets grew.
Additional Note, 1/18/99: In order to clarify some confusion on the SN1987A issue and light-speed, let me give another illustration that does not depend on the geometry of triangles etc. Remember, distances do not change with changing light-speed. Even though it is customary to give distances in light-years (LY), that distance is fixed even if light-speed c is changing.
To start, we note that it has been established that the distance from SN1987A to the sheet of material that reflected the peak intensity of the light burst from the SN, is 2 LY, a fixed distance. Imagine that this distance is subdivided into 24 equal light-months (LM). Again the LM is a fixed distance. Imagine further that as the peak of the light burst from the SN moved out towards the sheet of material, it emitted a pulse in the direction of the earth every time it passed a LM subdivision. After 24 LM subdivisions the peak burst reached the sheet.
Let us assume that there is no substantive change in light-speed from the time of the light-burst until the sheet becomes illuminated. Let us further assume for the sake of illustration, that the value of light-speed at the time of the outburst was 10c now. This means that the light-burst traversed the DISTANCE of 24 LM or 2 LY in a TIME of just 2.4 months. It further means that as the traveling light-burst emitted a pulse at each 1 LM subdivision, the series of pulses were emitted 1/10th month apart IN TIME.
However, as this series of pulses traveled to earth, the speed of light slowed down to its present value. It means that the information contained in those pulses now passes our earth-bound observers at a rate that is 10 times slower than the original event. Accordingly, the pulses arrive at earth spaced one month apart in time. Observers on earth assume that c is constant since the pulses were emitted at a DISTANCE of 1 LM apart and the pulses are spaced one month apart in TIME.
The conclusion is that this slow-motion effect makes it impossible to find the value of c at the moment of emission by this sort of process. By a similar line of reasoning, superluminal jets from quasars can be shown to pose just as much of a problem on the cDK model as on conventional theory. The standard explanation therefore is accepted here. (Thanks to Helen Fryman, January 14, 18, 1999)
Question: I've been following the dialog regarding the issue of the value of c at the location of supernova 1987A. I'm curious, how does one account for the constant gamma ray energies from known transitions (i.e. the same as in the earth's frame) and the neutrino fluxes (with the right kind of neutrinos at the expected energy) if c is significantly larger? Wasn't one of the first signals of this event a neutrino burst?
For example, if positron annihilation gammas were observed in the event and the value of the speed of light at 1987A was 10c, wouldn't you expect a hundredfold increase in the gamma energy from .511MeV to 51.1MeV?
Answer: Thanks for the question, its an old one. You have assumed in your question that other atomic constants have in fact remained constant as c has dropped with time. This is not the case. In our 1987 Report, Trevor Norman and I pointed out that a significant number of other atomic constants have been measured as changing lock-step with c during the 20th century. This change is in such a way that energy is conserved during the cDK process. All told, our Report lists 475 measurements of 11 other atomic quantities by 25 methods in dynamical time.
This has the consequence that in the standard equation [E = mc2] the energy E from any reaction is unchanged (within a quantum interval - which is the case in the example under discussion here). This happens because the measured values of the rest-mass, m, of atomic particles reveal that they are proportional to 1/(c2). The reason why this is so, is fully explored in the forthcoming redshift paper. Therefore in reactions from known transitions, such as occurred in SN1987A with the emission of gamma rays and neutrinos, the emission energy will be unchanged for a given reaction. I trust this reply is adequate. (Barry Setterfield, 1/21/99)
Question: Please bear with me once more as I attempt to come up to speed here. If the values of fundamental "constants" vary with location in the universe it implies that there are preferred reference frames. That is, a physicist could determine some absolute position relative to some origin because the "constants" vary as a function of position. If the "universal constants" are different at the position of supernova 1987A, for example, then the physics is different and an observer in that frame should be able to determine that he is in a unique position relative to any other frame of reference and vice-versa.
Are there observables to show this effect or are transformations proposed that make the physics invariant even with changing "constants?"
Answer: It is incorrect to say that the values of the fundamental constants vary with LOCATION in the cosmos. The cDK proposition maintains that at any INSTANT OF TIME, right throughout the whole cosmos, the value of any given atomic constant including light-speed, c, will be the same. There is thus no variation in the atomic constants with LOCATION in the universe. As a consequence there can be no preferred frame of reference. What we DO have is a variation of the atomic constants over TIME throughout the cosmos, but not LOCATION.
Because we look back in TIME as we probe deeper into space, we are seeing light emitted at progressively earlier epochs. The progressively increasing redshift of that light, as we look back in TIME, bears information on the value of some atomic constants and c in a way discussed in the forthcoming redshift paper. So Yes! there is a whole suite of data that can be used to back up this contention. I trust that clarifies the issue for you somewhat. (Barry Setterfield 1/23/99).
Notes on a Discussion with Prof. Frederick N. Skiff, Associate Professor of Physics, University of Maryland. *
When Barry Setterfield and Trevor Norman published their work on the speed of light decay in 1987, entitled "The Atomic Constants, Light and Time", it eventually sparked a great deal of controversy over not only the idea of the decay of the speed of light (cDK), but over the way the data had been handled by Setterfield and Norman. Accusations were made regarding mishandling data and pre-selecting data to fit their theories. The fact that data from such a limited time (since it had been possible to directly measure the speed of light) was, of necessity, used and then extrapolated backwards was also brought up. Because the earlier in time the light speed measurements had been taken, the more subject to error they were, there were a number of physicists who felt that no reliable curve could be fit to the data at all. Statistician Alan Montgomery looked at the data and, after working with it, came to the conclusion that the Setterfield-Norman paper was correct in its use of the data. [Much of the material concerning and explaining this can be found at Lambert Dolphin's website (http://ldolphin.org/constc.shtml)].
In the meantime, Douglas Kelly, in his book __ Creation and Change: Genesis 1.1 - 2.4 in the light of changing scientific paradigms__ (1997, Christian Focus Publications, Great Britain) discusses this issue in terms of Genesis. Endeavoring to present both sides of the cDK argument, he asked for a comment from Professor Frederick N. Skiff. Professor Skiff responded with a private letter which Kelly published on pp. 153 and 154 of his book. The letter is quoted below and, after that, Barry Setterfield responds.
* Current address: Prof. Frederick N. Skiff, Associate Professor of Physics, Department of Physics and Astronomy, 412 Van Allen Hall, Iowa City, IA 52242.
Helen Fryman
January 25, 1999
* * * *
From Professor Frederick N. Skiff:
I see that Setterfield does indeed propose that Planck's constant is also changing. Therefore, the fine structure constant 'a' could remain truly constant and the electron velocity in the atom could then change in a fashion proportional to the speed of light. His hypothesis is plausible.
My concern was that if you say 1) The speed of light is changing. And 2) The electron velocity in the atom is proportional to the speed of light, then you will generate an immediate objection from a physicist unless you add 3) Planck's constant is also changing in such a way as to keep the fine structure 'constant' constant.
The last statement is not a small addition. It indicates that his proposal involves a certain relations between the quantum theory (in the atom) and relativity theory (concerning the speed of light). The relation between these theories, in describing gravity, space and time, is recognized as one of the most important outstanding problems in physics. At present these theories cannot be fully reconciled, despite their many successes in describing a wide rang of phenomena. Thus, in a way, his proposal enters new territory rather than challenging current theory. Actually, the idea has been around for more than a decade, but it has not been pursued for lack of proof. My concerns are the following:
The measurements exist over a relatively short period of time. Over this period of time the speed changes by only a small amount. No matter how good the fit to the data is over the last few decades, it is very speculative to extrapolate such a curve over thousands of years unless there are other (stronger) arguments that suggest that he really has the right curve. The fact is that there are an infinite number of mathematical curves which fit the data perfectly (he does not seem to realize this in his article). On the other hand, we should doubt any theory which fits the data perfectly because we know that the data contain various kinds of errors (which have been estimated). Therefore the range of potential curves is even larger, because the data contain errors. There is clearly some kind of systematic effect, but not one that can be extrapolated with much confidence. The fact that his model is consistent with a biblical chronology is very interesting, but not conclusive (there are an infinite number of curves that would also agree with this chronology). The fact that he does propose a relative well known, and simply trigonometric function is also curious, but not conclusive.
The theoretical derivation that he gives for the variation of the speed of light contains a number of fundamental errors. He speaks of Planck's constant as the quantum unit of energy, but it is the quantum unit of angular motion. In his use of the conversion constant b he seems to implicitly infer that the 'basic' photon has a frequency of 1Hz, but there is no warrant for doing this. His use of the power density in an electromagnetic wave as a way of calculating the rate of change of the speed of light will not normally come out of a dynamical equation which assumes that the speed of light is a constant (Maxwell's Equations). If there is validity in his model, I don't believe that it will come from the theory that he gives. Unfortunately, the problem is much more complicated, because the creation is very rich in phenomena and delicate in structure.
Nevertheless, such an idea begs for an experimental test. The problem is that the predicted changes seem to be always smaller than what can be resolved. I share some of the concerns of the second respondent in the Pascal Notebook article.* One would not expect to have the rate of change of the speed of light related to the current state-of-the-art measurement (the graph of page 4 of Pascal's Notebook**) unless the effect is due to bias. Effects that are 'only there when you are not looking' can happen in certain contexts in quantum theory, but you would not expect them in such a measurement as the speed of light.
There are my concerns. I think that it is very important to explore alternative ideas. The community which is interested in looking at theories outside of the ideological mainstream is small and has a difficult life. No one scientist is likely to work out a new theory from scratch. It needs to be a community effort, I think.
Notes:
* A reference to "Decrease in the Velocity of Light: Its Meaning For Physics" in The Pascal Centre Notebook, Vol One, Number one, July, 1990. The second respondent to Setterfield's theory was Dr. Wytse Van Dijk, Professor of Physics and Mathematics, Redeemer College, who asked (concerning Professor Troistskii's model of the slowing down of the speed of light): 'Can we test the validity of Troitskii's model? If his model is correct, then atomic clocks should be slowing compared to dynamic clocks. The model could be tested by comparing atomic and gravitational time over several years to see whether they diverge. I think such a test would be worthwhile. The results might help us to resolve some of the issues relation to faith and science." ( p.5.)
** This graph consists of a correlation of accuracy of measurements of speed of light c with the rate of change in c between 1740 and 1980.
Barry Setterfield's response, January 25, 1999
During the early 1980's it was my privilege to collect data on the speed of light, c. In that time, several preliminary publications on the issue were presented. In them the data list increased with time as further experiments determining c were unearthed. Furthermore, the preferred curve to fit the data changed as the data list became more complete. In several notable cases, this process produced trails on the theoretical front and elsewhere which have long since been abandoned as further information came in. In August of 1987, our definitive Report on the data was issued as "The Atomic Constants, Light and Time" in a joint arrangement with SRI International and Flinders University. Trevor Norman and I spent some time making sure that we had all the facts and data available, and had treated it correctly statistically. In fact the Maths Department at Flinders Uni was anxious for us to present a seminar on the topic. That report presented all 163 measurements of c by 16 methods over the 300 years since 1675. We also examined all 475 measurements of 11 other c-related atomic quantities by 25 methods. These experimental data determined the theoretical approach to the topic. From them it became obvious that, with any variation of c, energy is going to be conserved in all atomic processes. A best fit curve to the data was presented.
In response to criticism, it was obvious the data list was beyond contention - we had included everything in our Report. Furthermore, the theoretical approach withstood scrutiny, except on the two issues of the redshift and gravitation. The main point of contention with the Report has been the statistical treatment of the data, and whether or not these data show a statistically significant decay in c over the last 300 years. Interestingly, all professional statistical comment agreed that a decay in c had occurred, while many less qualified statisticians claimed it had not! At that point, a Canadian statistician, Alan Montgomery, liaised with Lambert Dolphin and me, and argued the case well against all comers. He presented a series of papers which have withstood the criticism of both the Creationist community and others. From his treatment of the data it can be stated that c decay (cDK) has at least formal statistical significance.
However, my forthcoming redshift paper (which also resolves the gravitational problem) takes the available data right back beyond the last 300 years. In so doing, a complete theory of how cDK occurred (and why) has been developed in a way that is consistent with the observational data from astronomy and atomic physics. In simple terms, the light from distant galaxies is redshifted by progressively greater amounts the further out into space we look. This is also equivalent to looking back in time. As it turns out, the redshift of light includes a signature as to what the value of c was at the moment of emission. Using this signature, we then know precisely how c (and other c-related atomic constants) has behaved with time. In essence, we now have a data set that goes right back to the origin of the cosmos. This has allowed a definitive cDK curve to be constructed from the data and ultimate causes to be uncovered. It also allows all radiometric and other atomic dates to be corrected to read actual orbital time, since theory shows that cDK affects the run-rate of these clocks.
A very recent development on the cDK front has been the London Press announcement on November 15th, 1998, of the possibility of a significantly higher light-speed at the origin of the cosmos. I have been privileged to receive a 13 page pre-print of the Albrecht-Magueijo paper (A-M paper) which is entitled "A time varying speed of light as a solution to cosmological puzzles". From this fascinating paper, one can see that a very high initial c value really does answer a number of problems with Big Bang cosmology. My main reservation is that it is entirely theoretically based. It may be difficult to obtain observational support. As I read it, the A-M paper requires c to be at least 1060 times its current speed from the start of the Big Bang process until "a phase transition in c occurs, producing matter, and leaving the Universe very fine-tuned ...". At that transition, the A-M paper proposes that c dropped to its current value. By contrast, the redshift data suggests that cDK may have occurred over a longer time. Some specific questions relating to the cDK work have been raised. Penny wrote to me that someone had suggested "that the early measurements of c had such large probable errors attached, that (t)his inference of a changing light speed was unwarranted by the data." This statement may not be quite accurate, as Montgomery's analysis does not support this conclusion. However, the new data set from the redshift resolves all such understandable reservations.
There have been claims that I 'cooked' or mishandled the data by selecting figures that fit the theory. This can hardly apply to the 1987 Report as all the data is included. Even the Skeptics admitted that "it is much harder to accuse Setterfield of data selection in this Report". The accusation may have had some validity for the early incomplete data sets of the preliminary work, but I was reporting what I had at the time. The rigorous data analyses of Montgomery's papers subsequent to the 1987 Report have withstood all scrutiny on this point and positively support cDK. However, the redshift data in the forthcoming paper overcomes all such objections, as the trend is quite specific and follows a natural decay form unequivocally.
Finally, Douglas Kelly's book "Creation and Change" contained a very fair critique on cDK by Professor Fred Skiff. However, a few comments may be in order here to clarify the issue somewhat. Douglas Kelly appears to derive most of his information from my 1983 publication "The Velocity of Light and the Age of the Universe". He does not appear to reference the 1987 Report which updated all previous publications on the cDK issue. As a result, some of the information in this book is outdated. In the "Technical And Bibliographical Notes For Chapter Seven" on pp.153-155 several corrections are needed as a result. In the paragraph headed by "1. Barry Setterfield" the form of the decay curve presented there was updated in the 1987 Report, and has been further refined by the redshift work which has data back essentially to the curve's origin. As a result, a different date for creation emerges, one in accord with the text that Christ, the Apostles and Church Fathers used. Furthermore this new work gives a much better idea of the likely value for c at any given date. The redshift data indicate that the initial value of c was (2.54 x 1010) times the speed of light now. This appears conservative when compared with the initial value of c from the A-M paper of 1060 times c now.
Professor Skiff then makes several comments. He suggests that cDK may be acceptable if "Planck's constant is also changing in such a way as to keep the fine structure 'constant' constant." This is in fact the case as the 1987 Report makes clear.
Professor Skiff then addresses the problem of the accuracy of the measurements of c over the last 300 years. He rightly points out that there are a number of curves which fit the data. Even though the same comments still apply to the 1987 Report, I would point out that the curves and data that he is discussing are those offered in 1983, rather than those of 1987. It is unfortunate that the outcome of the more recent analyses by Montgomery are not even mentioned in Douglas Kelly's book.
Professor Skiff is also correct in pointing out that the extrapolation from the 300 years data is "very speculative". Nevertheless, geochronologists extrapolate by factors of up to 50 million to obtain dates of 5 billion years on the basis of less than a century's observations of half-lives. However, the Professor's legitimate concern here should be largely dissipated by the redshift results which take us back essentially to the origin of the curve and define the form of that curve unambiguously. The other issue that the Professor spends some time on is the theoretical derivation for cDK, and a basic photon idea which was used to support the preferred equation in the 1983 publication. Both that equation and the theoretical derivation were short-lived. The 1987 Report presented the revised scenario. The upcoming redshift paper has a completely defined curve, that has a solid observational basis throughout. The theory of why c decayed along with the associated changes in the related atomic constants, is rooted firmly in modern physics with only one very reasonable basic assumption needed. I trust that this forthcoming paper will be accepted as contributing something to our knowledge of the cosmos.
Professor Skiff also refers to the comments by Dr. Wytse Van Dijk who said that "If (t)his model is correct, then atomic clocks should be slowing compared to dynamical clocks." This has indeed been observed. In fact it is mentioned in our 1987 Report. There we point out that the lunar and planetary orbital periods, which comprise the dynamical clock, had been compared with atomic clocks from 1955 to 1981 by Van Flandern and others. Assessing the evidence in 1984, Dr. T. C. Van Flandern came to a conclusion. He stated that "the number of atomic seconds in a dynamical interval is becoming fewer. Presumably, if the result has any generality to it, this means that atomic phenomena are slowing with respect to dynamical phenomena ..." This is the observational evidence that Dr. Wytse Van Dijk and Professor Skiff required. Further details of this assessment by Van Flandern can be found in "Precision Measurements and Fundamental Constants II", pp.625-627, National Bureau of Standards (US) Special Publication 617 (1984), B. N. Taylor and W. D. Phillips editors.
In conclusion, I would like to thank Fred Skiff for his very gracious handling of the cDK situation as presented in Douglas Kelly's book. Even though the information on which it is based is outdated, Professor Skiff's critique is very gentlemanly and is deeply appreciated. If this example were to be followed by others, it would be everyone's advantage. (BARRY SETTERFIELD)
Question: Is the universe mature or does it just appear mature? Are there any ways to observationally differentiate between a mature universe and an apparently mature universe? If a globular cluster looks like it is 13 GY old and has a population of stars that give that appearance, it is 13 GY old for all intents and purposes. There is no difference. In this vein, why would God create a nearly dead star, a White dwarf, a core of a star that has had its atmosphere discharged in a planetary nebula episode after it has extinguished its nuclear fuel? Does God create all things new or would he create "old" dead objects. Was the soil in the garden of Eden filled with decaying vegetable and animal matter? Were there bones and fossils in the sediments below the soil? A dead star equates well with a fossil, I believe. Would God create either?
Response: Inherent within the redshift data for cDK is an implied age for the cosmos both on the atomic clock and on the dynamical or orbital clock. These ages are different because the two clocks are running at different rates. The atomic clock runs at a rate that is proportional to light speed, and can be assessed by the redshift. Originally this clock was ticking very rapidly, but has slowed over the history of the universe. By contrast, the dynamical or orbital clock runs at a uniform rate. The atomic clock, from the redshift data, has ticked off at least 15 billion atomic years. By contrast, the orbital clock, since the origin of the cosmos, has ticked off a number of years consistent with the patriarchal record in the Scriptures. (Barry Setterfield, 1/29/99)
Question: The ZPE levels quoted in Barry's paper, "Atomic Behavior, Light, and the Redshift" seem extraordinarily large. Secondly, Barry is predicting a large refraction of EM energy as it travels through space. But the cosmic background radiation shows no such refraction.
Response: The energy levels for the ZPE are standard figures. One quote in New Scientist some months back put it at 1098 ergs/cc, right in the middle of the range given here. Hal Puthoff has figures within that range.
There will be no refraction of electro-magnetic waves traveling through space because space is a non-dispersive medium. The key point that maintains this fact is the intrinsic impedance of space, Z*. This quantity Z* = 376.7 ohms. It has ALWAYS been 376.7 ohms. If there were a change in Z* with time, refraction would occur as it does when light enters another medium. Because the electric and magnetic vectors of a light wave are BOTH uniformly changing synchronously, Z* does not change. That results since both the permittivity and permeability of space (the two terms that make up Z*) are equally affected by ZPE changes. If only one was affected, as we had in our 1987 Report, there would be consequences that are not in accord with observation, and dispersion and/or refraction would occur." (added March 8, 1999)
Question: Has anyone done the calculations, based on your theory of changing speed of light, to see if the radiometric dating of fossils and rocks goes from the current value of billions of years down to thousands of years? Is it available on the Internet? Can you please give me a summary? Thank you.
ResponseThank you for your request for information. Yes, the calculations have been done to convert radiometric and other atomic dates to actual orbital years. This is done on the basis outlined in our Report of 1987 and the new paper just undergoing peer review. Basically, when light-speed is 10 times its current value, all atomic clocks ticked 10 times faster. As a consequence they registered an age of 10 atomic years when only one orbital year had passed. For all practical purposes there is no change in the rate of the orbital clocks with changing light speed. The earth still took a year to go around the sun.
Now the redshift of light from distant galaxies carries a signature in it that tells us what the value of c was at the time of emission. The redshift data then give us c values right back to the earliest days of the cosmos. Knowing the distances of these astronomical objects to a good approximation, then allows us to determine the behavior of light speed with time. It is then a simple matter to correct the atomic clock to read actual orbital time. Light speed was exceedingly fast in the early days of the cosmos, but dropped dramatically. At a distance of 20 billion light years, for example, the value of c was about 87 million times its current value. At that point in time the atomic clocks were ticking off 87 million years in just one ordinary year. When the process is integrated over the redshift/cDK curve the following approximate figures apply.
1 million years before present (BP) atomically is actually 2826 BC with c about 70,000 times c now.
63 million atomic years BP is an actual date of 3005 BC with c about 615,000 times c now.
230 million atomic years BP is an actual date of 3301 BC with c about 1.1 million times c now.
600 million atomic years BP is an actual date of 3536 BC with c about 2.6 million times c now.
2.5 billion atomic years BP is an actual date of 4136 BC with c about 10.8 million times c now.
4.5 billion atomic years BP is an actual date of 4505 BC with c about 19.6 million times c now.
15 billion atomic years BP is an actual date near 5650 BC with c about 65.3 million times c now.
20 billion atomic years BP is an actual date near 5800
BC with c about 87 million times c now.
Question from Ron Samec: I might be repeating my self. But, the Decreasing Speed of Light Model (DSLM) has to not only to take into account photons, i.e., radiation, but they have to deal with matter also. It was the neutrinos, now believed to have mass, that first gave us the signal that Super Novae 1987a. The Star had collapsed and crushed protons and electrons into neutrons at a distance of 170,000 or so Light Years. The folks that espouse the Mature Creation Model (MCM) have to have the history of the explosion be "written into" the radiation and now the matter stream that came to us form the direction of the Large Magellanic Cloud. Of course, in the MCM, this never really "happened". It just appears that it happened. To the DSLM people, the neutrinos would give them an increasing rest mass (or rest energy if you like) as we go back into history. (Of course this effects all matter. If we believe in the conservation of energy, where has all this energy gone?) The Neutrinos would have been decreasing in rest mass as they traveled through space. Thus they would be radiating. Since Neutrinos permeate the universe in fantastic numbers, this radiation should be detectable. But, what we wold detect would be a continuum of frequencies, not a single temperature, 3 degree, cosmic background radiation. If the speed of light enabled light waves to travel 10 billion light years in a day or so, this means light would be traveling 100,000 times faster. The rest mass would be 10 billion times larger! How do they deal with this? One other problem is that the radiation carries momentum varying with the speed of light.
Response from Barry: It really does appear as if Ron Samec has not done his homework properly on the cDK (or DSLM) issue that he discussed in relation to Super Nova 1987 A. He pointed out that neutrinos gave the first signal that the star was exploding, and that neutrinos are now known to have mass. He then goes on to state (incorrectly) that neutrinos would have an increasing rest mass (or rest energy) as we go BACK into history. He then asks "if we believe in the conservation of energy, where has all this energy gone?" He concluded that this energy must have been radiated away and so should be detectable. Incredibly, Ron has got the whole thing round the wrong way. If he had read our 1987 Report, he would have realized that the observational data forced us to conclude that with cDK there is also conservation of energy. As the speed of light DECREASES with time, the rest mass will INCREASE with time. This can be seen from the Einstein relation [E = mc2]. For Energy E to remain constant, the rest mass m will INCREASE with time in proportion to [1/ (c2)] as c is dropping. This INCREASE in rest-mass with time has been experimentally supported by the data as listed in Table 14 of our 1987 Report. There is thus no surplus energy to radiate away at all, contrary to Ron's suggestion, and the rest-mass problem that he poses will also disappear.
In a similar way, light photons would not radiate energy in transit as their speed drops. According to experimental evidence from the early 20th century when c was measured as varying, it was shown that wavelengths, [w], of light in transit are unaffected by changes in c. Now the speed of light is given by [c = fw] where [f] is light frequency. It is thus apparent that as [c] drops, so does the frequency [f], as [w] is unchanged. The energy of a light photon is then given by [E = hf] where [h] is Planck's constant. Experimental evidence listed in Tables 15A and 15B in the 1987 Report as well as the theoretical development shows that [h] is proportional to [1/c] so that [hc] is an absolute constant. This latter is supported by evidence from light from distant galaxies. As a result, since [h] is proportional to [1/c] and [f] is proportional to [c], then [E = hf] must be a constant for photons in transit. Thus there is no extra radiation to be emitted by photons in transit as light-speed slows down, contrary to Ron's suggestion, as there is no extra energy for the photon to get rid of.
I hope that this clarifies the matter for Ron and others. I do suggest that the 1987 Report be looked at in order to see what physical quantities were changing, and in what way, so that any misunderstanding of the real situation as given by observational evidence can be avoided. This Report is now available for viewing at 1987 Report, (http://ldolphin.org/setterfield/report.html). Note that there are several sections that have been updated in the new Redshift Paper and have accordingly been omitted in order to avoid confusion. Thank you for your time and interest. (May 13, 1999)
Question:
E=energy, v = speed, m = ordinary mass, c = speed of light, p = momentum, sqrt=square root
Setterfield states that the E is conserved so the mass of a particle has to increase as c2 decreases. So mc2 is a constant. But, for a moving mass particle, E = gamma X mc2, where gamma is the stretch factor, 1/sqrt(1-v2/c2). The stretch factor would decrease greatly since the ratio of v/c would decrease since c would increase. I suppose Barry will counter that by saying that if the neutrino is traveling at 0.99 c before it will be traveling at 0.99 c afterward. Only the quantity, c, changes. At this point we are talking about something different, mechanical energy. We are talking about speeding the particle up. How do we do that? We have to introduce a new constant, it is pc, the particle momentum times the speed of light. How does that come about? If c decreases, p has to increase in a nice direct inverse proportionality. So we have mc2 and pc are constants. I am certain there are other interesting things. Off the top of my head (I don't have time, as you mention, to do much home work, after all, I am a busy physics professor that only gives homework!), The wavelength of matter particles is h/p, the DeBroglie wavelength. The wavelength of matter waves like an electron or neutrino will change. Did old electron microscopes have a different magnification (resolution power)? What about waves in the microscopic world, ordinary light waves? The momentum imparted by a light wave must increase greatly, p = I/c (I is the intensity).The rate for energy flux of a wave (the Poynting vector) as proportional to the Field energy times the wave speed. If the wave speed was much larger, the energy delivered by the wave would be much greater. This would greatly effect the solar constant, for instance, increasing the energy impinging on the Earth by a large degree... There must be many more of these, but I have to get back to work. Can we assume Barry has looked into all the Electromagnetic ramifications and solved them all? I have a copy of his 1987 paper and I will look into it!
(In my old suggested problem of a Neutrino traveling from a neutron formation in Super Novae 1987a, If the speed of light enabled light waves to travel 10 billion light years in a day or so, this means light would be traveling 100,000 times faster. According to Barry's theory, the mass of a traveling neutrino would decrease by a factor of 10 billion times! This really makes a missing mass problem!)
RESPONSE: I appreciate the problem that you have with your "homework"! Forgive me for being so hard on you! However, if nothing else, it might have given you some appreciation as to how your students fell about the matter! Since particle momentum [p = mc] where [m] is particle mass and [c] is light-speed, and as [mc2] is a constant so that [m] is proportional to [1/(c2)], then it follows that [p] is indeed proportional to [1/c]. In other words, your conclusion that [pc] is conserved is correct.
However, you have not followed through so well on the DeBroglie wavelengths [W] of matter. The relationship is indeed [W = h/(mc) = h/p]. Now it has just been shown above that [p = mc] is proportional to [1/c]. Furthermore, it was also pointed out in my previous posting that Planck's constant [h] is also proportional to [1/c] so that hc is an absolute constant throughout the cosmos. This is something that has been observationally verified. Therefore with both [h] and [p] being proportional to [1/c], it follows that [h/p = W] will be a constant. Your additional comment about light waves and other waves being affected as a consequence is also out of order. You might recall my earlier comment that experiments done while light was measured as dropping revealed that wavelengths were NOT affected by the process, which is why the frequency must vary with c, and not wavelengths.
In your concluding section that was in brackets, you suggest there was a huge missing mass problem as every neutrino or atomic particle was so much less massive back in the early days of our Cosmos. This turns out not to be the case, however, as the gravitational constant [G] is changing in such a way that [Gm = constant]. This also means that gravitational acceleration [g] and hence weight will be unaffected by the process. Note too that in all orbit equations the second mass (that of the orbiting body) appears on both sides of the equation and so cancels out leaving only the [Gm] term.
Therefore, planetary orbits will not be affected by the cDK process. Then there was a final cluster of questions relating to momenta of light waves, the Poynting vector, the solar constant and energy impinging on earth from the sun etc. First, as you pointed out the momentum [p] of a light wave is equal to [J/c] where [J] is the intensity. (Note that I have changed your [I] to [J] to avoid confusion of similar letters.) For light in transit where [c] is dropping, this means that the momentum of a photon at reception will be greater than that at emission. But as that effect is happening for every other light wave of given intensity [J], including those in our laboratories, nothing out of the ordinary will be noticed.
This leads on to the second matter relating to the Poynting vector. The Poynting vector [S] is equal to the energy density [U] of the electromagnetic wave multiplied by [c]. Thus we write [S = Uc]. However, the value of [U] is determined by the magnetic permeability and electric permittivity of free space. Now since both the permeability and permittivity of free space are proportional to [1/c], it can be shown that [U] is also proportional to [1/c]. Therefore, for light in transit, [Uc = constant = S]. I would ask you to note here that the most recent work has confirmed that BOTH the permittivity AND the permeability of space must be changing, unlike the approach in the 1987 Report which had only the permeability varying. Finally, there is the matter of the output of energy by the sun and stars, and radioactive sources. The Redshift paper undergoing review at the moment points out that when c was higher, the emitted radiation energy densities were lower as shown by the behavior of [U] above. In addition, the radiation was comprised of photons whose energy was also intrinsically lower (that is redshifted compared with today's laboratory standard). When these effects are taken into account, radiation from radioactive sources, and the output of energy from the sun and stars is more prolific now than it was then. The mathematical details are in the redshift paper. I trust that this answers your queries satisfactorily. (May 14, 1999)
Question If mass is changing via E = m c2 with E constant for a given object or particle, and c changing, the m varies inversely with c squared. So larger c values in the past mean smaller masses. Now, for binary stars or any two orbiting bodies, the sum of the masses in solar mass units of the component stars equals the semimajor axis cubed divided by the orbital period squared (Kepler's Harmonic Law). If the mass decreases the orbital periods lengthen. Back into time, orbital periods were longer. In fact, orbital periods go as c squared. That means that the Earth's year was longer (by about a billion times in the beginning). Changing masses would also effect the Cepheid Variable star periods and therefor the cosmic distance scale. There are a myriad of effects if we think about gravity. Planets, stars etc. would not hold together in the beginning. Maybe Barry has G increasing into the past also, to take care of these problems. Perhaps the quantity Gm is also a constant along with mc2 and pc. I will read his 1987 writeup.
Response from Barry: It appears as if I did not make a key point as plain as I would have liked in my previous posting. If I had, I could have saved you most of the heartache of your latest posting. Let me reiterate what it was that I said. "...the gravitational constant [G] is changing in such a way that [Gm = constant]. This means that the gravitational acceleration [g] and hence weight will be unaffected by the process. Note too that in all orbit equations the secondary mass (that of the orbiting body) appears on both sides of the equation and so cancels out leaving only the [Gm] term. Therefore planetary orbits will not be affected by the cDK process. ..." This is not only the case for planetary orbits, but stellar orbits as well. Therefore Ron has correctly deduced, after his initial bout of problems, that [Gm] is in fact a constant. A full treatment of this is given in the Redshift paper rather than the 1987 Report, although the [G] data set appears there. Note that as [Gm] occurs in our equations as a single entity, no variation in [G] and [m] separately can be found by gravitational dependent methods. The other matters that Ron raised were all on the basis of a constant [G]. Since this is not the scenario being presented, those problems essentially disappear with [Gm = constant]. (May 14, 1999)
Questions on the Minimum Value of c. (May 15, 1999).
Two Comments and Responses: Ron Samec has suggested in one of his postings that what may have been discovered is not a change in the value of c over the past 100 years, but rather "a secular change in the index of refraction of the atmosphere" due to the industrial revolution.
Bless him for the thought! But it is not original! This issue was discussed in the literature when c was actually measured as varying. In Nature, page 892 for June 13, 1931, V. S. Vrkljan answered this question in some detail. The kernel of what he had to say is this: "...a simple calculation shows that within the last fifty years the index of refraction [of the atmosphere] should have increased by some [6.7 x10-4] in order to produce the observed decrease [in c] of 200 km/sec. According to Landolt-Bornstein (Physikalisch-chemische Tabellen, vol.ii, 1923, p.959, I Erganzungsband, Tracking or intellectual phase locking and cDK In another one of his [newsgroup] postings on this topic, Ron Samec has suggested that the decay in c might be due merely to "tracking" or intellectual phase locking. This process is described as one in which the values of a physical constant become locked around a canonical value obtained by some expert in the field. Because of the high regard for the expert, other lesser experimenters will tailor their results to be in agreement with the value obtained by the expert. As a result, other experiments to determine the value of the constant will only slowly converge to the correct value.
Although this charge may be leveled at some high school and first year university students, it is an accusation of intellectual dishonesty when brought into the arena of the cDK measurements. First, there was a continuing discussion in the scientific literature as to why the measured values of c were decreasing with time. It was a recognized phenomena. In October of 1944, N. E. Dorsey summarized the situation. He admitted that the idea of c decay had "called forth many papers." He went on to state that "As is well-known to those acquainted with the several determinations of the velocity of light, the definitive values successively reported ... have, in general, decreased monotonously from Cornu's 300.4 megametres per second in 1874 to Anderson's 299.776 in 1940 ..." Dorsey strenuously searched for an explanation from the journals that the various experimenters had kept of their determinations. All he could do was to extend the error limits and hope that this covered the problem. In Nature for April 4, 1931, Gheury de Bray commented: "If the velocity of light is constant, how is it that, INVARIABLY, new determinations give values which are lower than the last one obtained. ... There are twenty-two coincidences in favour of a decrease of the velocity of light, while there is not a single one against it." (his emphasis).
In order to show the true situation, one only has to look at the three different experiments that were running concurrently in 1882. There was no collusion between the experimenters either during the experiments or prior to publication of their results. What happened? In 1882.7 Newcomb produced a value of 299,860 km/s. In 1882.8 Michelson produced a value of 299,853 km/s. Finally in 1883, Nyren obtained a value of 299,850 km/s. These three independent authorities produced results that were consistent to within 10 km/sec. This is not intellectual phase locking or tracking; these are consistent yet independent results from three different recognized authorities. Nor is this a unique phenomenon. Newcomb himself noted that those working independently around 1740 obtained results that were broadly in agreement, but reluctantly concluded that they indicated c was about 1% higher than in his own time. In 1941 history repeated itself when Birge made a parallel statement while writing about the c values obtained by Newcomb, Michelson and others around 1880. Birge was forced to concede that "...these older results are entirely consistent among themselves, but their average is nearly 100 km/s greater than that given by the eight more recent results."
In view of the fact that these experimenters were not lesser scientists, but were themselves the big names in the field, they had no canonical value to uphold. They were themselves the authorities trying to determine what was happening to a capricious "constant". The figures from Michelson tell the story here. His first determination in 1879 gave a value of 299,910 km/s. His second in 1883 gave a result of 299,853 km/s. In 1924 he obtained a value of 299,802 km/s while in 1927 it was 299,798 km/s. This is not intellectual phase locking. Nor is it typical of a normal distribution about a fixed value. What usually happens when a fixed constant is measured is that the variety of experiments give results that are scattered about a fixed point. Instead, when all the c results are in, there is indeed a scatter; yet that scatter is not about a fixed point, but about a declining curve. It is a phenomenon that intellectual phase locking cannot adequately explain. If Dorsey, Birge or Newcomb could have explained it that way, we would certainly have heard about it in the scientific literature of the time. (May 20, 1999)
Question: Since about 1960 the speed of light has been measured with tremendous precision with no observed change. Proponents of cDK usually reply that we have redefined units of measurement in such a way that when the modern methods of measurement are used the change in c disappears because of cancellation. Has anyone attempted to remeasure c by "old fashioned" methods? It would seem to me that redoing the classic measurements could settle this issue, at least to my satisfaction. This would provide a new baseline of at least four decades, and probably much more.
Response: The problem with current methods of light-speed measurements (mainly laser) is that both wavelengths [W] and frequency [F] are measured to give c as the equation reads [c = FW]. If you have followed the discussion well, you will be aware that, within a quantum interval, wavelengths are invariant with any change in c. This means that it is the frequency of light that varies lock-step with c. Unfortunately, atomic frequencies also vary lock-step with c, so that when laser frequencies are measured with atomic clocks no difference will be found.
The way out of this is to use some experimental method where this problem is avoided. Ron Samec has suggested that the Roemer method may be used. This method uses eclipse times of Jupiter's inner satellite Io. Indeed it has been investigated by Eugene Chaffin. Although many things can be said about his investigation (and they may be appropriate at a later date), there are a couple of outstanding problems which confronts all investigators using that method. Chaffin pointed out that perturbations by Saturn, and resonance between Io, Europa, and Ganymede are definitely affecting the result, and a large number of parameters therefore need investigation. Even after that has been done, there remains inherent within the observations themselves a standard deviation ranging from about 30 to 40 seconds. This means the results will have an intrinsic error of up to 24,000 km/s. Upon reflection, all that can be said is that this method is too inaccurate to give anything more than a ball-park figure for c, which Roemer to his credit did, despite the opposition. It therefore seems unwise to dismiss the cDK proposition on the basis of one of the least precise methods of c measurement as the notice proposes that was brought to our attention by Ron. This leaves a variety of other methods to investigate.
However, that is not the only way of determining what is happening to c. There are a number of other physical constants which are c-dependent that overcome the problem with the use of atomic clocks. One of these is quantized Hall Resistance now called the von Klitzing constant. Another might be the gyromagnetic ratio. A further method is to compare dynamical intervals (for example, using Lunar radar or laser ranging) with atomic intervals. These and other similar quantities give an indication that c may have bottomed out around 1980 and is slowly increasing again. Indeed, atomic clock comparisons with historical data can be used to determine the behavior of c way back beyond 1675 AD when Roemer made the first determination. These data seem to indicate that c reached a maximum around 700 AD (very approximately). The data from the redshift paper implies that this oscillation is superimposed on an exponential decline in the value of c from the early days of the cosmos. A more complete discussion appears in the redshift paper. In other words, whole new sets of data are becoming available from additional sources that allow the original proposition to be refined. I trust that you find this helpful.(May 20, 1999).
Measurement Methods: I was thinking more in terms of a Fizzeau device, which is what I assumed was used by Newcomb and the others mentioned in your earlier comments.
Response: Your suggestion is a good one. Either the toothed wheel or the rotating mirror experiments should give a value for c that is free from the problems associated with the atomic clock/frequency blockage of modern methods, and the shortcomings of the Roemer method. The toothed wheel requires a rather long base-line to get accurate results as shown by the experiments themselves. However, given that limitation, an interesting feature may be commented upon. Cornu in 1874.8 and Perrotin in 1901.4 essentially used the same equipment. The Cornu mean is 299,945 km/s while the Perrotin mean is 299,887 km/s. This is a drop of 58 km/s in 26.6 years measured by the same equipment.
The rotating mirror experiments also required a long base-line, but the light path could be folded in various ways. Michelson in 1924 chose a method that combined the best features of both the rotating mirror and toothed wheel: it was the polygonal mirror. In the 1924 series, Michelson used an octagonal mirror. Just over two years later, in 1926.5 he decided to use a variety of polygons in a second series of experiments. The glass octagon gave 299,799 km/s; the steel octagon 299,797 km/s; a 12 faced prism had 299,798 km/s; a 12 faced steel prism gave 299,798 km/s; and a 16 faced glass prism resulted in a value of 299,798 km/s. In other words all the polygons were in agreement to within +/-- 1 km/s and about 1,600 individual experiments had been performed. That is a rather impressive result. However, despite the internal accuracy to within 1 km/s, these results are still nearly 6.5 km/s above the currently accepted value.
To my way of thinking, this polygonal mirror method would probably be the best option for a new determination of c. On the other hand, perhaps Newcomb's or Michelson's apparatus from earlier determinations may still be held in a museum display somewhere. Modern results from such apparatus would certainly arouse interest. Thanks for the helpful suggestion.
On the Measurement of Time, and the Velocity of Light:Several questions have been raised by John Hill which deserve a reply.
First, the matter of timing and clocks. In 1820 a committee of French scientists recommended that day-lengths throughout the year be averaged, to what is called the mean solar day. The second was then defined as 1/86,400 of this mean solar day. This definition was accepted by most countries and supplied science with an internationally accepted standard of time. This definition was used right up until 1956. In that year it was decided that the dynamical definition of a second be changed to become 1/31,556,925.97474 of the earth's orbital period that began at noon on the 1st January 1900. Note that this definition of the second ensured that the second remained the same length of time as it had always been right from its earlier definition in 1820. This definition continued until 1967 when atomic time became standard. The point to note is that in 1967 one second on the atomic clock was DEFINED as being equal to the length of the dynamical second, even though the atomic clock is based on electron transitions. Interestingly, the vast majority of c measurements were made in the period 1820 to 1967 when the actual length of the second had not changed. Therefore, the decline in c during that period cannot be attributed to changes in the definition of a second.
However, changes in atomic clock rates affecting the measured value for c will certainly occur post 1967. In actual fact, the phasing-in period for this new system was not complete until January 1, 1972. It is important to note that dynamical or orbital time is still used by astronomers. However, the atomic clock which astronomers now use to measure this has leap-seconds added periodically to synchronize the two clocks. The International Earth Rotation Service (IERS) regulates this procedure. Since January 1st, 1972, until January 1st, 1999 exactly 32 leap seconds have been added to keep the two clocks synchronized. There are a number of explanations as to why this one-sided procedure has been necessary. Most have to do with changes in the earth's rotational period. However, a contributory cause MAY be the change in light-speed, and the consequent change in run-rate of the atomic clock. If it is accepted that it is the run-rate of the atomic clock which has changed by these 32 seconds in 27 years, then this corresponds to a change in light-speed of exactly [32/(8.52032 x 108) c = (3.7557 x 10-8 c ] or close to 11.26 meters/second.
The question then becomes, "Is this a likely possibility?" Many scientists would probably say no. However, Lunar and planetary orbital periods which comprise the dynamical clock, have been compared with atomic clocks from 1955 to 1981 by Van Flandern and others. Assessing the evidence in 1981 Van Flandern noted that "the number of atomic seconds in a dynamical interval is becoming fewer. Presumably, if the result has any generality to it, this means that atomic phenomena are slowing down with respect to dynamical phenomena." (Precision Measurements and Fundamental Constants II, pp. 625-627, National Bureau of Standards (US) Special Publication 617, 1984. Even if these results are controversial, Van Flandern's research at least establishes the principle on which the former comments were made.
Note here that, given the relationship between c and the atomic clock, it can be said that the atomic clock is extraordinarily PRECISE as it can measure down to less than one part in 10 billion. However, even if it is precise, it may not be ACCURATE as its run-rate will vary with c. Thus a distinction has to be made between precision and accuracy when talking about atomic clocks.
Finally, John had some concerns about timing devices used on any future experiments to determine c by the older methods. Basically, all that is needed is an accurate counter that can measure the number of revolutions of a toothed wheel or a polygonal prism precisely enough in a one second period while light travels over a measured distance. Obviously the higher the number of teeth or mirror faces the more accurate the result. Fizeau in 1849 had a wheel with 720 teeth that rotated at 25.2 turns per second. In 1924, Michelson rotated an octagonal mirror at 528 turns per second. We should be able to do better than both of those now and minimize any errors. The measurement of the second could be done with accurate clocks from the mid-50's or early 60's. This procedure would probably overcome most of the problems that John foresees in such an experiment. If John has continuing problems, please let us know.
Further Comments on Time Measurements and c: In 1820 a committee of French scientists recommended that day lengths throughout the year be averaged, to what is called the Mean Solar Day. The second was then defined as 1/86,400 of this mean solar day. This supplied science with an internationally accepted standard of time. This definition was used right up to 1956. In that year it was decided that the definition of the second be changed to become 1/31,556,925.97474 of the earth's orbital period that began at noon on 1st January 1900. This definition continued until 1967 when atomic time became standard. In 1883 clocks in each town and city were set to their local mean solar noon, so every individual city had its own local time. It was the vast American railroad system that caused a change in that. On 11th October 1883, a General Time Convention of the railways divided the United States into four time zones, each of which would observe uniform time, with a difference of precisely one hour from one zone to another. Later in 1883, an international conference in Washington extended this system to cover the whole earth.
The key point to note here is that the vast majority of c measurements were made during the period 1820 to 1956. During that period there was a measured change in the value of c from about 299,990 km/s down to 299,792 km/s, a drop of the order of 200 km/s in 136 years. The question is what component of that may be attributable to changes in the length of the second since the rate of rotation of the earth is involved in the existing definition. It is here that the International Earth Rotation Service (IERS) comes into the picture. Since 1st January 1972 until 1st January 1999, exactly 32 leap seconds have been added to keep Co-ordinated Universal Time (UTC) synchronized with International Atomic Time (TAI) as a result of changes in the earth's rotation rate. Let us assume that these 32 leap seconds in 27 years represent a good average rate for the changes over the whole period of 136 years from 1820 to 1956. This rate corresponds to an average change in measured light-speed of [32/(8.52023 x 108) c = (3.7557 x 10-8) c] or close to 11.26 meters per second in one year. As 136 years are involved at this rate we find that [11.26 x 136 = 1531] meters per second or 1.53 km/s over the full 136 years. This is less than 1/100th of the observed change in that period. As a result it can be stated (as I think Froome and Essen did in their book "The Velocity of Light and Radio Waves") that limitations on the definition of the second did not impair the measurement of c during that period ending in 1956.
Therefore, if measurements of c were done with modern equivalents of rotating mirrors, toothed wheels or polygonal prisms, and the measurements of seconds were done with accurate equipment from the 1950's, a good comparison of c values should be obtained. Note, however, that the distance that the light beam travels over should be measured by equipment made prior to October 1983. At that time c was declared a universal constant (299,792.458 km/s) and, as such, was used to re-define the meter in those terms.
As a result of the new definitions from 1983, a change in c would also mean a change in the length of the new meter compared with the old. However, this process will only give the variation in c from the change-over date of 1983. By contrast, use of some of the old experimental techniques measuring c will allow direct comparisons back to at least the early 1900's and perhaps earlier. In a similar way, comparisons between orbital and atomic clocks should pick up variations in c. As pointed out before, this latter technique has in fact been demonstrated to register changes in the run-rate of the atomic clock compared with the orbital clock by Van Flandern in the period 1955 to 1981.
By way of further information, the meter was originally introduced into France on the 22nd of June, 1799, and enforced by law on the 22nd of December 1799. This "Meter of the Archives" was the distance between the end faces of a platinum bar. In September 1889 up till 1960 the meter was defined as the distance between two engraved lines on a platinum-iridium bar held at the International Bureau of Weights and Measures in Sevres, France. This more recent platinum-iridium standard of 1889 is specifically stated to have reproduced the old meter within the accuracy then possible, namely about one part in a million. Then in 1960, the meter was re-defined in terms of the wavelength of a krypton 86 transition. The accuracy of lasers had rendered a new definition necessary in 1983. It can therefore be stated that from about 1800 up to 1960 there was no essential change in the length of the meter. It was during that time that c was measured as varying. As a consequence, the observed variation in c can have nothing to do with variations in the standard meter.(Barry Setterfield, May 29, 1999)
Question: If light velocity has not always been a constant "c", why can it be mathematically shown to be constant even from distant star light? (ie. wavelength (m) x frequency (1/s)= 2.99792 x 108m/s) this equation is consistent even when the variables are changed! Light speed (velocity is constant)
Answer from Barry: It has been proved recently by aberration experiments that distant starlight from remote galaxies arrives at earth with the same velocity as light does from local sources. This occurs because the speed of light depends on the properties of the vacuum. If we assume that the vacuum is homogeneous and isotropic (that is has the same properties uniformly everywhere at any given instant), then light-speed will have the same value right throughout the vacuum at any given instant. The following proposition will also hold. If the properties of the vacuum are smoothly changing with time, then light speed will also smoothly change with time right throughout the cosmos.
On the basis of experimental evidence from the 1920's when light speed was measured as varying, this proposition maintains that the wavelengths of emitted light do not change in transit when light-speed varies, but the frequency (the number of wave-crests passing per second) will. The frequency of light in a changing c scenario is proportional to c itself. Imagine light of a given earth laboratory wavelength emitted from a distant galaxy where c was 10 times the value it has now. The wavelength would be unchanged, but the emitted frequency would be 10 times greater as the wave-crests are passing 10 times faster. As light slowed in transit, the frequency also slowed, until when it reaches earth at c now, the frequency would be the same as our laboratory standard as well as the wavelength. Trust that this reply answers your question. (June 15, 1999)
Question: Photons possess many different energy levels. From radio waves to gamma rays. Are these "categories" dependent on wavelength or energy? If it is dependent on wave length (as all radio-technology would insist on)then sometime in the future there will be much less light and lower wavelength photons, and much more radio waves. Will we all someday be blind?
Response: The energy of a photon E is given by [hf] or [hc/w] where h is Planck's constant, f is frequency, w is wavelength, and c is light-speed. Two situations exist. First, for LIGHT IN TRANSIT through space. As light-speed drops with time, h increases so that [hc] is a constant. It should be emphasized that frequency, [f], is simply the number of wave-crests that pass a given point per second. Now wavelengths [w] in transit do not change. Therefore, as light-speed c is dropping, it necessarily follows that the frequency [f] will drop in proportion to c as the number of wave-crests passing a given point will be less, since [c = fw]. Since [f] is therefore proportional to c, and [h] is proportional to [1/c], it follows that [hf] is a constant for light in transit. Since both [hc] and [w] are also constants for light in transit, this means that [hc/w] and [hf] do not alter. In other words, for light in transit, E the energy of a photon is constant, other factors being equal.
The second situation is that pertaining at the TIME OF EMISSION. When c is higher, atomic orbit energies are lower. This happens in a series of quantum steps for the atom. Light-speed is not quantized, but atomic orbits are. As light-speed goes progressively higher the further we look back into space, so atomic orbit energies become progressively lower in quantum steps. This lower energy means that the emitted photon has less energy, and therefore the wavelength [w] is longer (redder). This lower photon energy is offset by proportionally more photons being emitted per unit time. So the total energy output remains essentially unchanged.
As a result of these processes at emission, light from distant galaxies will appear redder (the observed redshift), but there will be more photons so distant sources will appear to be more active than nearby ones. Both of these effects are observed astronomically. (Barry Setterfield, August 1, 1999)
Question: One of the most interesting things I read in your article is that the wavelength of light partakes in expansion in transit through space. I believe you referenced the Astrophysical Journal 429:491-498, 10 July, 1994.
I don't have immediate access to this journal. It was mentioned almost as a side issue, I want to know if you agree with it and how it serves your theory if you do. I'm also interested in the physical reasoning, observation, and mathematics of the journal article itself. Thank you.
Response Yes! According to the Friedmann model of the universe, which is basically Einsteinian, as space expands, the wavelengths of light in transit become stretched also. This is how the redshift of light from distant galaxies is accounted for by standard Big Bang cosmology. The reference is correct, but any serious text on the redshift will give the same story. This does not serve our theory except for one point. The redshift has been shown by Tifft to be quantized. It goes in jumps of about 2.7 km/s. It is very difficult to account for this by a smooth expansion of space. Alternatively, if the quantization is accepted as an intrinsic feature of emitted wavelengths (rather than wavelengths in transit), it means that the cosmos cannot be expanding (or contracting) as the exact quantizations would be "smeared out" as the wavelengths stretched or contracted in transit.
Question: Can you estimate how many total quantum jumps in c have occurred since creation? Could this give us a kind of "cosmic clock" ticking out some kind of absolute time scale?
Response I doubt if you could call such a clock "The Clock of the LORD" as it does not tick off regular intervals. The decay in c is essentially exponential, and each quantum change occurs once c has dropped by about 600 times its present value. Under these conditions, it becomes apparent that the initial intervals on that proposed clock are passing much more quickly than now if assessed by our usual gravitational or dynamical or orbital clock. As for the number of quantum jumps that have occurred, the most distant objects seen by Hubble Space telescope are around z = 14. This gives a light speed around [9.21 x 108] c now. This means about 1,536,317 quantum changes. (Note that z and the quantum change relationship is absolutely fixed. The exact change in light-speed per quantum change is somewhat more indefinite, being dependent upon what value is placed on the Hubble constant.) Note also that light-speed does not itself jump down a quantum number as it is a smooth function. Once light-speed has changed by about 600 times its present value, a quantum jump in atomic phenomena will occur. As for the total number of quantum changes, that depends on the initial value of c and the exact relationship between the drop in c and the quantum change. From Van Flandern's gravitational data that will be about [2 x 1010) c now. Our redshift data curve suggests a value around [2.5 x 1010] c now. If these data are being handled correctly, that will give a total number of quantum changes of about 41.5 million. The problem is we do not have an exact redshift value for the origin of the cosmos, so a precise number of quantum changes cannot yet be given. However, these figures suggest an original redshift value close to [z = 375], but as yet we cannot be absolutely sure.
Question for Statistician Alan Montgomery: I have yet to read a refutation of Aardsma's weighted uncertainties analysis in a peer reviewed Creation journal. He came to the conclusion that the speed of light has been a constant. --A Bible college science Professor.
Reply from Alan Montgomery: The correspondent has commented that nobody has refuted Dr. Aardsma work in the ICR Impact article.
In Aardsma's work he took 163 data from Barry Setterfield's monograph of 1987 and put a weighted regression line through the data. He found that the rate of decrease was negative but the deviation from zero was only about one standard deviation. This would normally not be regarded as significant enough to draw a statistical conclusion.
In my 1994 ICC paper I demonstrated among other things the foolishness of using all the data--those methods with and without sensitivity to the data to the question. You cannot use a ruler to measure the size of a bacteria. Second, I demonstrated that 92 of the data he used were not corrected to in vacuo and therefore his data was a bad mixture. One cannot draw firm conclusions from such a statistical test.
I must point out to the uninitiated in statistical studies that there is a difference between a regression line and a regression model. A regression model attempts to provide a viable statistical estimate of the function which the data exhibits. The requirements of a model are that it must be:
(1) a minimum variance (condition met by a regression line);
(2) homoskedastic - data are of the same variance (condition met by a weighted linear regression) and
(3) it must not be autocorrelated - the residuals must not leave a non-random pattern .
My paper thus went a step further in identifying a proper statistical representation of the data. If I did not point it out in my paper, I will point it out here. Aardsma's weighted regression line was autocorrelated and thus shows that the first two conditions and the data imposed a result which is undesirable if one is trying to mimic the data with a function. The data is not evenly distributed and the weights are not evenly distributed. These biases are such that the final 11 data determine the line almost completely. This being so caution must be exercised in interpreting the results. Considering the bias in the weights and their small size, data with any significant deviation from them should not be used. It adds a great deal of variance to the line yet never adds any contribution to its trend. In other words, the highly precise data determines the direction and size of the slope and the very low imprecision data makes any result statistically insignificant. Aardsma's results are not so much wrong as unreliable for interpretation.
The Professor may draw whatever conclusions he likes about Aardsma's work but those who disagree with the hypothesis of decreasing c have rarely mentioned his work since. I believe for good reason.
Alan Montgomery (amontgo@osfi-bsif.gc.ca), October 14, 1999.
Note added by Brad Sparks: I happened to be visiting ICR and Gerry Aardsma just before his first Acts & Facts article came out attacking Setterfield. I didn't know what he was going to write but I did notice a graph pinned on his wall. I immediately saw that the graph was heavily biased to hide above-c values because the scale of the graph made the points overlap and appear to be only a few points instead of dozens. I objected to this representation and Aardsma responded by saying it was too late to fix, it was already in press. It was never corrected in any other forum later on either, to my knowledge.
What is reasonable evidence for a decrease in c that would be convincing to you? Do you require that every single data point would have to be above the current value of c? Or perhaps you require validation by mainstream science, rather than any particular type or quality of evidence. We have corresponded in the past on Hugh Ross and we seemed to be in agreement. Ross' position is essentially that there could not possibly ever be any linguistic evidence in the Bible to overturn his view that "yom" in the Creation Account meant long periods; his position is not falsifiable. This is the equivalent of saying that there is no Hebrew word that could have been used for 24-hour day in Genesis 1 ("yom" is the only Hebrew word for 24-hour day and Ross is saying it could not possibly mean that in Gen. 1). Likewise, you seem to be saying there is no conceivable evidence even possible hypothetically for a decrease in c, a position that is not falsifiable. If I'm misunderstanding you here please set me straight. Brad Sparks, October 14, 1999
Malcolm Bowden Comments: Robert Hill says he has not seen a criticism of Chaffins ICC paper. In my CENTJ article of v12 n 1 1998 pp 48-54 I pointed out Chaffins two errors. I also have given this in my "True Science Agrees with the Bible." p304.
Chaffin clearly did not want to accept CDK because he completely turned logic on its head on two occasions.
ICC 1990 p 47-52 : Lieske's work indicated that CDK HAD taken place. He then said without the slightest justification - "But suppose that Lieske was too conservative...Then it would be possible to conclude that the speed of light 300 years ago was the same as today." My comment was that if we can ignore any contrary evidence, ANYTHING can be concluded.
ICC 1994 pp143-150: Bradley's results. Chaffin varied his computer and found that a best fit was when c was 2.4% higher than today. He dismissed this by saying they were not accurate enough to determine whether c was higher. If the results were that poor he should not have even tried to measure c by this method. Yet the method DID show c was faster in the past with fair accuracy. He was hoping that the figures would not show an increase but in fact they did and he therefore had to dismiss them in some way. If they had shown a constant one would guess that he would have reported this.
Not one of the commentators on this paper referred to these illogical arguments he used. Malcolm Bowden, (mb@mbowden.info)
Question from Malcolm Bowden: In your reply about the formation of the geological column, you said- "In other words, the geological column has been formed over a 3000 year period since Creation. A similar statement can be made for radiometric ages of astronomical bodies, like the Moon, or meteorites." The Bible says the Flood lasted for about one year. So how could it have been formed "over 3,000 years"?
Response: A couple of points need to be made. First, the redshift observations show a systematic decrease in the speed of light. In fact the redshift data have allowed the cDK curve to be formulated with some exactness. It is a smooth exponential-type decline with a very small oscillation superimposed. As a result of the redshift data, the value of light-speed at any time in the past can be fairly closely determined.
Second, it is established from the physics of the situation that some atomic processes, including radiometric decay are light-speed dependent. More correctly, both light-speed and radioactive decay are mutually affected by the increasing energy density of the ZPE. Thus, as light-speed is smoothly dropping with time, so is the rate of radioactive decay upon which radiometric dates are dependent. The redshift data reveal that the bulk of this decay has occurred over a 3000 year period during which predicted radiometric ages dropped from 14 billion years down to a few thousand years on the atomic clock. More particularly, the Cryptozoic strata formed over a period of 2250 years, while the Phanerozoic strata formed over a period of 750 years.
The third point follows on from these two. You cannot account for all the radiometrically dated strata in a 1 year period. The whole process took close to 3000 years according to the redshift data. As a consequence, the data point to the geological column being formed by a series of catastrophes and their ongoing processes over three millennia rather than one catastrophe lasting just 1 year. If you turn the argument around the other way, one may predict that the strata from the Flood would date radiometrically from about 650 million years and younger. The Babel incident would correspond to events around 245 million years atomically, while the Peleg continental division would occur about 65 million years ago on the atomic clock. These are all significant atomic dates in the geological column.
Fourth, if you want to account for the bulk of the geological column and its dates in just one year, that would require the observed redshift sequence to undergo a massive jump at a set distance in space. This is certainly not observed. Likewise the value of light-speed would have to undergo a dramatic drop, a discontinuity, which the data do not reveal.
Fifth, the redshift data do something else. Evolutionists have been puzzled by some interesting facts. The asteroid impacts that ended the Mesozoic would have been expected to wipe out the dinosaurs. Yet a few dinosaurs were still there up to 2 million atomic years after the impact. They cannot account for this. However, the redshift data explains why. The speed of light at that point in time was about 500,000 times its current speed, so that 2 million years were just 4 years of actual time - soon enough after the catastrophe and the changing conditions it brought. The second puzzle that evolutionists have that has received a lot of attention in the Creationist press is the so-called "discordant" radiometric dates. There is a good reason for this, too. During much of the Palaeozoic, light-speed was around 1.5 to 2 million times its current speed. That means that the radiometric clocks ticked off about 2 million years in one orbital year. If a granite pluton was intruded into strata being laid down at that time, its interior would take some considerable time to cool. Time of the order of 10 years or more may not be unreasonable. That will give a spread of 20 million years in the dates from that structure. This might be considered to be an error of up to 10% in the radiometric date, when in reality it is quite accurate.
Finally, there is a problem facing Creationists who require the majority of the geological column to be built up at the time of the Flood. In the first place, throughout the fossil record there are many examples of creatures eating each other. According to Genesis 9:3-5 compared with Genesis 1:29-30 and Genesis 6:21, the diet of all creatures was vegetarian until after the Flood. Therefore, fossils of creatures eating other creatures must be post-Flood if the Scripture is to have any relevance on this matter.
In the second instance, the fossil record poses some significant problems in another way. The mammoths of Siberia were buried near the surface, virtually in situ. Yet they are underlain by thousands of feet of sediments, some fossiliferous. If their demise was in the Flood, where were they during the first few months when those sediments were being laid, and how did their food supply have time to germinate and flourish since they obviously did not starve to death? A similar problem exists with the Paluxy dinosaurs. These Mesozoic prints overlie thousands of feet of Palaeozoic sediments. Their food supply and method of survival during the first few months of the Flood while surrounded with water is a conundrum, unless they perished in a separate disaster in the days of Peleg.
This problem of in situ fossils is repeated many times throughout the geological column. It cannot be explained by the ecological zoning argument, nor the action of turbidity currents and sorting. In Europe, eggs from dinosaurs such as Protoceretops are found in their nests. Other dinosaurs were entombed by windstorms that built up the Mesozoic desert dune systems. In each case they lay on top of Palaeozoic sediments. These Mesozoic sands in Europe and the USA are nearly all of non-marine origin. However, they all lie on top of marine Palaeozoic sequences. Such wind-blown sand systems take time to develop, as do the annual layers of dinosaurs nests found in them. So do the many coral deposits that overlie Palaeozoic strata. This model based on the redshift data allows these fossil species to develop in situ on top of existing sediments and then be preserved in a separate (Scriptural) catastrophe.
As a consequence, the redshift model necessitates a re-think of some basic Creationist traditions which are not necessarily supported by Scripture. Yes the Flood lasted one year, but the Scripture does not say that all the geological strata formed at that time. I am acutely aware that this will be most unsatisfactory to many creationists who have supported the traditional Model over the years, but it really does seem to overcome a lot of problems which that Model has. We may yet have to put this new wine into new wineskins. But let's see how things develop. I trust that this answers the question. (October 22, 1999).
Question: I heard that there is published evidence that the Red Shift is quantized. Can you explain this in lay terms?
Response: The following quotation concerning this phenomenon is from "Quantized Galaxy Redshifts" by William G. Tifft & W. John Cocke, University of Arizona, Sky & Telescope Magazine, Jan., 1987, pgs. 19-21: As the turn of the next century approaches, we again find an established science in trouble trying to explain the behavior of the natural world. This time the problem is in cosmology, the study of the structure and "evolution" of the universe as revealed by its largest physical systems, galaxies and clusters of galaxies. A growing body of observations suggests that one of the most fundamental assumptions of cosmology is wrong.
Most galaxies' spectral lines are shifted toward the red, or longer wavelength, end of the spectrum. Edwin Hubble showed in 1929 that the more distant the galaxy, the larger this "redshift". Astronomers traditionally have interpreted the redshift as a Doppler shift induced as the galaxies recede from us within an expanding universe. For that reason, the redshift is usually expressed as a velocity in kilometers per second.
One of the first indications that there might be a problem with this picture came in the early 1970's. William G. Tifft, University of Arizona noticed a curious and unexpected relationship between a galaxy's morphological classification (Hubble type), brightness, and red shift. The galaxies in the Coma Cluster, for example, seemed to arrange themselves along sloping bands in a redshift vs. brightness diagram. Moreover, the spirals tended to have higher redshifts than elliptical galaxies. Clusters other than Coma exhibited the same strange relationships.
By far the most intriguing result of these initial studies was the suggestion that galaxy redshifts take on preferred or "quantized" values. First revealed in the Coma Cluster redshift v.s. brightness diagram, it appeared as if redshifts were in some way analogous to the energy levels within atoms.
These discoveries led to the suspicion that a galaxy's redshift may not be related to its Hubble velocity alone. If the redshift is entirely or partially non-Doppler (that is, not due to cosmic expansion), then it could be an intrinsic property of a galaxy, as basic a characteristic as its mass or luminosity. If so, might it truly be quantized?
Clearly, new and independent data were needed to carry this investigation further. The next step involved examining the rotation curves of individual spiral galaxies. Such curves indicate how the rotational velocity of the material in the galaxy's disk varies with distance from the center.
Several well-studied galaxies, including M51 and NGC 2903, exhibited two distinct redshifts. Velocity breaks, or discontinuities, occurred at the nuclei of these galaxies. Even more fascinating was the observation that the jump in redshift between the spiral arms always tended to be around 72 kilometers per second, no matter which galaxy was considered. Later studies indicated that velocity breaks could also occur at intervals that were 1/2, 1/3, or 1/6 of the original 72 km per second value.
At first glance it might seem that a 72 km per second discontinuity should have been obvious much earlier, but such was not the case. The accuracy of the data then available was insufficient to show the effect clearly. More importantly, there was no reason to expect such behavior, and therefore no reason to look for it. But once the concept was defined, the ground work was laid for further investigations.
The first papers in which this startling new evidence was presented were not warmly embraced by the astronomical community. Indeed, an article in the Astrophysical Journal carried a rare note from the editor pointing out that the referees "neither could find obvious errors with the analysis nor felt that they could enthusiastically endorse publication." Recognizing the far-reaching cosmological implications of the single-galaxy results, and undaunted by criticism from those still favoring the conventional view, the analysis was extended to pairs of galaxies.
Two galaxies physically associated with one another offer the ideal test for redshift quantization; they represent the simplest possible system. According to conventional dynamics, the two objects are in orbital motion about each other. Therefore, any difference in redshift between the galaxies in a pair should merely reflect the difference in their orbital velocities along the same line of sight. If we observe many pairs covering a wide range of viewing angles and orbital geometries, the expected distribution of redshift differences should be a smooth curve. In other words, if redshift is solely a Doppler effect, then the differences between the measured values for members of pairs should show no jumps.
But this is not the situation at all. In various analyses the differences in redshift between pairs of galaxies tend to be quantized rather than continuously distributed. The redshift differences bunch up near multiples of 72 km per second. Initial tests of this result were carried out using available visible-light spectra, but these data were not sufficiently accurate to confirm the discovery with confidence. All that changed in 1980 when Steven Peterson, using telescopes at the National Radio Astronomy Observatory and Arecibo, published a radio survey of binary galaxies made in the 21-cm emission of neutral hydrogen.
Wavelength shifts can be pegged much more precisely for the 21cm line than for lines in the visible portion of the spectrum. Specifically, redshifts at 21 cm can be measured with an accuracy better than the 20 km per second required to detect clearly a 72 km per second periodicity.
Red shift differences between pairs group around 72, 144 and 216 km per second. Probability theory tells us that there are only a few chances in a thousand that such clumping is accidental. In 1982 an updated study of radio pairs and a review of close visible pairs demonstrated this same periodic pattern at similarly high significance levels.
Radio astronomers have examined groups of galaxies as well as pairs. There is no reason why the quantization should not apply to larger collections of galaxies, so redshift differentials within small groups were collected and analyzed. Again a strongly periodic pattern was confirmed.
The tests described so far have been limited to small physical systems; each group or pair occupies only a tiny region of the sky. Such tests say nothing about the properties of redshifts over the entire sky. Experiments on a very large scale are certainly possible, but they are much more difficult to carry out.
One complication arises from having to measure galaxy redshifts from a moving platform. The motion of the solar system, assuming a doppler interpretation, adds a real component to every redshift. When objects lie close together in the sky, as with pairs and groups, this solar motion cancels out when one redshift is subtracted from another, but when galaxies from different regions of the sky are compared, such a simple adjustment can no longer be made. Nor can we apply the difference technique; when more than a few galaxies are involved, there are simply too many combinations. Instead we must perform a statistical test using redshifts themselves.
As these first all-sky redshift studies began, there was no assurance that the quantization rules already discovered for pairs and groups would apply across the universe. After all, galaxies that were physically related were no longer being compared. Once again it was necessary to begin with the simplest available systems. A small sample of dwarf irregular galaxies spread around the sky was selected.
Dwarf irregular galaxies are low-mass systems that have a significant fraction of their mass tied up in neutral hydrogen gas. They have little organized internal or rotational motion and so present few complications in the interpretation of their redshifts. In these modest collections of stars we might expect any underlying quantum rules to be the least complex. Early 20th century physicists chose a similar approach when they began their studies of atomic structure; they first looked at hydrogen, the simplest atom.
The analysis of dwarf irregulars was revised and improved when an extensive 21-cm redshift survey of dwarf galaxies was published by J. Richard Fisher and R. Brent Tully. Once the velocity of the solar system was accounted for, the irregulars in the Fisher-Tully Catalogue displayed an extraordinary clumping of redshifts. Instead of spreading smoothly over a range of values, the redshifts appeared to fall into discrete bins separated by intervals of 24 km per second, just 1/3 of the original 72 km per second interval. The Fisher-Tully redshifts are accurate to about 5 km per second. At this small level of uncertainty the likelihood that such clumping would randomly occur is just a few parts in 100,000.
Large-scale redshift quantization needed to be confirmed by analyzing redshifts of an entirely different class of objects. Galaxies in the Fisher-Tully catalogue that showed large amounts of rotation and interval motion (the opposite extreme from the dwarf irregulars) were studied.
Remarkably, using the same solar-motion correction as before, the galaxies' redshifts again bunched around certain specific values. But this time the favored redshifts were separated by exactly 1/2 of the basic 72 km per second interval. This is clearly evident. Even allowing for this change to a 36 km per second interval, the chance of accidentally producing such a preference is less than 4 in 1000. It is therefore concluded that at least some classes of galaxy redshifts are quantized in steps that are simple fractions of 72 km per second.
Current cosmological models cannot explain this grouping of galaxy redshifts around discrete values across the breadth of the universe. As further data are amassed the discrepancies from the conventional picture will only worsen. If so, dramatic changes in our concepts of large-scale gravitation, the origin and "evolution" of galaxies, and the entire formulation of cosmology would be required.
Several ways can be conceived to explain this quantization. As noted earlier, a galaxy's' redshift may not be a Doppler shift, it is the currently commonly accepted interpretation of the red shift, but there can be and are other interpretations. A galaxy's' redshift may be a fundamental property of the galaxy. Each may have a specific state governed by laws, analogues to those in quantum mechanics that specify which energy states atoms may occupy. Since there is relatively little blurring on the quantization between galaxies, any real motions would have to be small in this model. Galaxies would not move away from one another; the universe would be static instead of expanding.
This model obviously has implications for our understanding of redshift patterns within and among galaxies. In particular it may solve the so-called "missing mass" problem. Conventional analysis of cluster dynamics suggest that there is not enough luminous matter to gravitationally bind moving galaxies to the system.
Question: I looked at several papers published after Humphreys', yet found only ONE reference to it. The objections that Humphreys raised have not been answered by Setterfield, Montgomery, Dolphin, Bowden or anyone else that I can see. If I have missed it then please let me know.
The one reference I did find was this from Montgomery: "Humphreys [14, p42] questioned why the rate of decrease of c should decrease in direct proportion to our ability to measure it. Humphreys gave no evidence that this was true."
But if you read Humphreys CRSQ paper, he DID give evidence that this was true - in the sentences IMMEDIATELY preceding the reference that Montgomery cites above! Furthermore, the very next sentence in Montgomery's paper says: "As yet no paper has properly addressed this important issue of the sensitivity of the data" - which is essentially admitting that this is a problem!
There was also another vague reference to Humphreys' personal correspondence with Goldstein over the Roemer data. Bowden pointed out that Goldstein himself seems to have bungled some of his calculations and that Mammel has corrected them. But the point Humphreys was making in his paper was that Setterfield was using a 2nd hand quotation and didn't bother to check with the source, or do his own verification. Indeed, it was Mammel who found the problems with Goldstein's calculations not Setterfield or Bowden.
Response from Alan Montgomery: At the time I presented my Pittsburgh paper (1994) I looked at Humphreys paper carefully as I knew that comments on the previous analyses was going to be made mandatory. It became very apparent to me that Humphreys was relying heavily on Aardsma's flawed regression line. Furthermore, Aardsma had not done any analysis to prove that his weighted regression line made sense and was not some vagary of the data. Humphreys paper was long on opinion and physics but he did nothing I would call an analysis. I saw absolutely nothing in the way of statistics which required response. In fact, the lack of anything substantial statistical backup was an obvious flaw in the paper. To back up what he says requires that the areas where the decrease in c is observed is defined and where it is constant. If Humphreys is right the c decreasing area should be early and the c constant area should be late. There may be ambiguous areas in between. This he did not do. I repeat that Humphreys expressed an opinion but did not demonstrate statistically that it was true.
Secondly, Humphreys argument that the apparent decrease in c can be explained by gradually decreasing errors was explicitly tested for in my paper. The data was sorted by error bar size and regression lines were put through the data. By the mid-twentieth century the regression lines appeared to go insignificant. But then in the post 1945 data, the decrease became significant again in complete contradiction to his hypothesis. I would ask you who has in the last 5 years explained that? Name one person!
Third, the aberration values not only decrease to the accepted value but decrease even further. If Humphreys explanation is true why would those values continue to decrease? Why would those values continue to decrease in a quadratic just as the non-aberration values and why would the coefficients of the quadratic functions of a weighted regression line be almost identical and this despite the fact that the aberration and non-aberration data have highly disparate weights, centers of range and domain and weighted range and domain?
Fourth, if what Humphreys claims is true why are there many exceptions to his rule? Example, the Kerr Cell data is significantly below the accepted value. Therefore according to Humphreys there should be a slow increasing trend back to the accepted value. This simply is not true. The next values take a remarkable jump and then decrease. Humphreys made not even an attempt to explain this phenomenon, Why?
Humphreys paper is not at all acceptable as a statistical analysis. My statement merely reflected the truth about what he had not done. His explanation is a post hoc rationalization.
The physics I leave up to Lambert if he wants to comments on Humphreys physics. 11/10/99.
Comment to Question raised by Andrew Kulikovsky: I have recently talked to Mr. Setterfield and he has referenced CRSQ vol 25, March 1989, as his response to the argument brought up by Andrew regarding the aberration measurements. The following two paragraphs are a the direct quote from this part of the Setterfield response to the articles published in previous editions by Aardsma, Humphreys, and Holt critiquing the Norman-Setterfield 1987 paper . This part of the response is from page 194. After having read this, I am at a loss to understand why anyone would say Setterfield has not responded regarding this issue.
"In the [1987] Report it is noted at the bottom of Table 3 that the aberration constant is disputed. There is a systematic error that involves different techniques in Europe to those at Washington and is enhanced by the large number of twilight observations at Pulkova. The details are too lengthy to discuss here. The Washington aberration constant is now accepted as definitive resulting in systematically low c values from the European observations. When this error is corrected for, many values of c in Table 3 increase by about 230 km/s, with some higher. This correction overcomes the perceived problem with Figure I. The zero takes account of this systematic error and is thus not misleading, nor is the decay trend spurious, and the vast majority of values in Table 3 are then above c.
"The aberration values are very useful. The majority of Russian observations were done on the same instrument with the same errors. They display the decay trend well, which cannot be due to instrumental effects nor error reduction. The same comments apply to the results obtained from the Flower Observatory as well as the International Latitude Service. All give decay rates above 4 km/s per year. Far from being 'misleading,' the aberration values only serve to confirm the decay hypothesis."
References for the above:
Simon Newcomb, "The Elements of the Four Inner Planets and the Fundamental Constants of Astronomy," in the Supplement to the American Ephemeris and Nautical Almanac for 1897, p. 138 (Washington)
E.T. Whittaker, "Histories of Theories of Ether and Electricity," vol. 1, pp 23, 95 (1910, Dublin)
K.A. Kulikov, "Fundamental Constants of Astronomy," pp 81-96 and 191-195, translated from Russian and published for NASA by the Israel Program for Scientific Translations, Jerusalem. Original dated Moscow 1955. (submitted by Helen Fryman, [tuppence@NS.NET] November 13, 1999)
Question: When will the next quantized red-shift jump occur? Will there be any evidence of it that would affect everyday life?
Answer: The next quantum jump cannot be predicted until we know if the c decay curve has bottomed out. Data suggests it did around 1980. If that is the case, then c is increasing and the next quantum jump may be almost two millennia away. If, however, the decay in c continues for any length of time, it is possible that the next quantum jump may be relatively soon. The main evidence affecting everyday life may perhaps be earthquakes on all fault-lines around the planet.
Earthquakes are possible because there is a discrete change in the mass of atomic particles at the quantum jump. This has no effect gravitationally as gm is a constant. However, for a spinning body, if angular momentum is to be maintained, the small, discrete mass change would probably place a torque on the earth. This in turn would very marginally change our rotation rate. The stress which this process would place on fault lines across the planet would probably be relieved by earthquakes.
As to evidence for this behavior, several distant pulsars have been known to undergo starquakes and a change in spin rate, and it is possible that a quantum change may be the cause. There are several historical incidents which correspond approximately to quantum change dates on the cdk curve. However, much more work needs to be done on this area.
Question: Are you saying that 'c' is no longer decaying? (assuming the velocity of light has decreased exponentially to nearly zero at the present time.) Do you mean "nearly zero" compared to what it may have been at the time of creation?
Answer: The exponential decay has an oscillation superimposed upon it. The oscillation only became prominent as the exponential declined. The oscillation appears to have bottomed out about 1980 or thereabouts. If that is the case (and we need more data to determine this exactly) then light-speed should be starting to increase again. The minimum value for light-speed was about 0.6 times its present value. This is as close to 'zero' at it came.
Question: What does this mean in plain English? "Time after creation, in orbital years is approximately, D = 1499 t2". You state later that the age of the cosmos is approximately 8000 years (6000 BC + 2000 AD). How is this derived from the formula?
Answer: This formula only applies on a small part of the curve as it drops towards its minimum. Note that "d" is atomic time. Furthermore, 't' or orbital time, must be added to 2800 bc to give the actual BC date. The reason for this is that 2800 BC is approximately the time of the light-speed minimum.
The more general formula is "d = [1905 t2] + 63 million". In this formula "d" is atomic time, and once the value for "t" has been found it is added to 3005 bc to give the actual BC date. This is done because the main part of the curve starts about 3005 BC when the atomic clock is already registering 63 million years. Working in the reverse, therefore, if we take a date of 5790 BC we must first subtract 3005. This gives a value for "t" of 2785 orbital years. When 2785 is squared this gives 7.756 million. This is then multiplied by 1905 to obtain 14.775 billion. From this figure is then subtracted 63 million to give a final figure of 14.71 billion. This is the age in years that would have been registered on the atomic clock of an object formed in 5790 BC. (Barry Setterfield, January 23, 2000)
A Series of Questions from one Correspondent
Question #1: Setterfield assumes that the beginning of the universe is (from the moment We can observe anything at all) very small, hot, dense in energy and very rapidly expanding. Somewhere else he said (if I understood it right) that after two days the universe had its maximum size. Is that right?
Reply: I have assumed that at the very beginning of the cosmos it was in a small, hot dense state for two reasons. First, there is the observational evidence from the microwave background. Second there is the repeated testimony of Scripture that the lord formed the heavens and "stretched them out." I have not personally stipulated that this stretching out was completed by day 2 of Creation week. That has come from Lambert Dolphin's interpretation of events. What we can say is that it was complete by the end of the 6th day. It may well have been that the stretching out process was completed by the end of the first day from a variety of considerations. I have yet to do further thinking on that. Notice that any such stretching out would have been an adiabatic process, so the larger the cosmos was stretched, the cooler it became. We know the final temperature of space, around 2.7 degrees Absolute, so if it has been stretched out as the scripture states, then it must have been small and hot, and therefore dense initially, as all the material in the cosmos was confined in that initial hot ball.
Question #2: In expanding so rapidly there was a conversion of potential energy to the ZPE (what is the difference between zero-point energy and zero-point radiation?). This was not completed in two days but needed a longer period of time, about 3000 years (?)
Reply: Please distinguish here between what was happening to the material within the cosmos, and the very fabric of the cosmos itself, the structure of space. The expansion cooled the material enclosed within the vacuum allowing the formation of stars and galaxies. By contrast, the fabric of space was being stretched. This stretching gave rise to a tension, or stress within the fabric of space itself, just like a rubber band that has been expanded. This stress is a form of potential energy. Over the complete time since creation until recently, that stress or tension has exponentially changed its form into the zero-point energy (ZPE). The ZPE manifests itself as a special type of radiation, the zero-point radiation (ZPR) which is comprised of electromagnetic fields, the zero-point-fields (ZPF). These fields give space its unique character.
Question #3: Connected to this there was also a rapid decline in the speed of light, Because higher ZPE level puts a kind of "brake" on the speed of light because of higher permeability and permittivity (OK?).
Reply: Yes! As more tensional energy (potential energy) became exponentially converted into the ZPE (a form of kinetic energy), the permittivity and permeability of the vacuum of space increased, and light-speed dropped accordingly.
Question #4: As more energy came available in the world space, matters had to run at a higher energy level, causing the emitted light spectrum to be shifted in the blue direction.
Reply: Yes! It has been shown by Harold Puthoff in 1987 that it is the ZPE which maintains the particles in their orbits in every atom in the cosmos. When there was more ZPE, or the energy density of the ZPF became higher, each and Every atomic orbit took up a higher energy level. Each orbit radius remained fixed, but the energy of each orbit was proportionally greater. Light emitted from all atomic processes was therefore more energetic, or bluer. This process happened in jumps as atomic processes are quantized.
Question #5: Let me think what that means for the redshift case. Stars and galaxies not too distant have sent their original more redshifted light to the earth Already a long time ago. Now they sent only the "standard" spectrum.
Reply: Yes! The stars within our own milky way galaxy will not exhibit any quantum redshift changes. The first change will be at the distance of the Magellanic clouds. However, even out as far as the Andromeda nebula (part of our local group of galaxies and 2 million light-years away) the quantum redshift is small compared with the actual Doppler shift of their motion, And so will be difficult to observe.
Question: #6 Very distant galaxies have still not succeeded in sending us all their "redshifted" light, but this will reach us in due time (how long? Millions of years, I suspect?). This must be the reason that the redshift increases with greater distance of the stars.
Reply: That is correct! Because these distant galaxies are so far away their emitted light is taking a long time to reach us. This light was therefore emitted when atoms were not so energetic and so is redder than now. Essentially we are looking back in time as we look out to the distant galaxies, and the further we look back in time, the redder was the emitted Light. The light from the most distant objects comes from about 20 billion light-years away. This light has reached us in 7,700 years. The light initially traveled very fast, something like 1010 times its current speed, But has been slowing in transit as the energy density (and hence the permittivity and permeability) of space has increased.
Question #7: Is there any answer to the question if the light of even the most distant galaxies has reached the earth from the very beginning? Is there any reasoning for it?
Reply: Yes! There is an answer. When the speed of light was about 1010 times its current speed as it was initially, observers on earth could see objects 76,000 light years away by the end of the first day of creation week. That is about the diameter of our galaxy. Therefore the intense burst of light from the centre of our galaxy could be seen half way through the first day of creation week. This intense burst of light came from the Quasar-like processes that occurred in the centre of every galaxy initially.
Every galaxy had ultra-brilliant, hyperactive centers; ours was no exception. After one month light from galaxies 2.3 million light years Away would be visible from earth. This is the approximate radius of our local group of galaxies. So the Andromeda spiral galaxy would be visible by then. After one year, objects 27 million light-years away would be visible if telescopes were employed. We now can see to very great distances. However, since we do not know the exact size of the cosmos, we do not know if we can see right back to the "beginning."
Question #8: That this redshift caused by the rising ZPE level goes in jumps is clear to me, it is caused by the quantum-like behavior of matter.
Reply: Absolutely correct!
Question #9: Setterfield mentions the "highly energetic" beginning of the universe, but The ZPE was low at that time. How was this early energy represented? In a kind of "proto-matter" or something like that?
Reply: The highly energetic beginning of the universe was referring to the contents of the cosmos, the fiery ball of matter-energy that was the raw material that God made out of nothing, that gave rise to stars and galaxies as it cooled by the stretching out process. By contrast, the ZPE was low, Because the tensional energy in the fabric of space had not changed its form into the ZPE. A distinction must be made here between the condition of the contents of the cosmos and the situation with regards to the fabric of space itself. Two different things are being discussed. Note that at the beginning the energy in the fabric of space was potential energy from the stretching out process. This started to change its form into radiation (the ZPE) in an exponential fashion. As the tensional potential energy changed its form, the ZPE increased. (Barry Setterfield, February 24, 2000).
A Comment from a Skeptic:As for the physical problems with the c-decay model, probably the easiest refutation for the layman to understand invokes probably the only science equation that is well known by all, e = m c2. Let us imagine, if you will, that we have doubled the speed of light [the c constant]. That would increase e by a factor of 4. The heat output of the sun would be 4 times as hot. And you thought we had a global warming problem now. In other words, if the speed of light was previously higher (and especially if it was exponentially higher), the earth would've been fried a long time ago and no life would have been able to exist.
Reply: In the 1987 Report which is on these web pages, we show that atomic rest masses "m" are proportional to 1/(c2). Thus when c was higher, rest masses were lower. As a consequence the energy output of stars etc from the (E = m c2) reactions is constant over time when c is varying. Furthermore, it can be shown that the product Gm is invariant for all values of c and m. Since all the orbital and gravitational equations contain G m, there is no change in gravitational phenomena. The secondary mass in these equations appears on both sides of the equation and thereby drops out of the calculation. Thus orbit times and the gravitational acceleration g are all invariant. This is treated in more detail in my forthcoming paper, but is already in summary form on this web-site. (Barry Setterfield, 3/11/00)
A response to Robert P. J. Day's essay appearing in Talk Origins, (http://www.talkorigins.org/faqs/c-decay.html).
An article written by Robert P. J. Day, copyrighted 1997, has been posted for some time on the Talk Origins Archive. This article purports to debunk my research regarding the speed of light. However, except for one lone sentence, the entire essay is based on a series of progress reports that preceded the August 1987 paper written at the request of Stanford Research Institute. For Day to prefer to critique, in 1997, articles representative only of work in progress even before the Report itself was published (ten years before Day's article was copyrighted) shows how inappropriate his methods of research and criticism are.
The only statement that Robert Day has made that has any real relevance to the current discussion over c-decay is his mention of the Acts and Facts Impact article for June 1988 issued by Gerald Aardsma for the ICR. Aardsma's incorrect methodology was pointed out to him by several individuals before he even published the article. He arguments were also effectively rebutted by Trevor Norman, who was in the Math Dept. of Flinders University. Norman's rebuttal was based on a superior statistical approach recommended by the then Professor of Statistics in his Department. Aardsma never fully addressed the issues raised by Norman, and neither did several other statistical detractors. Furthermore, following an extensive series of analyses, Alan Montgomery presented two articles, one at a Creationist Conference (ICC 1994 Proceedings), the other in Galilean Electrodynamics (Vol.4 No.5 [1993] p 93 and following), that effectively silenced all statistical criticism of the c-decay proposition. Montgomery's two articles have never been refuted.
Day's criticism of my acknowledgment of my presuppositions is interesting. Is he decrying my honesty or the presuppositions themselves? He is welcome to disagree with them, but in return I would ask him to admit his own presuppositions, which I find I disagree with. As a Christian I do accept God's Word, or Scripture, as authoritative on the issues it addresses. Thus it is reasonable that I would be interested in pursuing an area of research which addresses some of these matters. I am not infallible and do not claim to have all the facts here. But the same situation prevails in any field of scientific endeavor, and that is why research continues. In the meantime, progress in data collection, observational evidence, and subsequent updating of a theory is very different from Day's mockery of a person's faith. I am wondering if his mockery may be a last resort when the legitimate scientific criticism was effectively answered long before the copyright date of 1997 on Day's article.
It should also be noted that a number of qualified scientists who do not share my beliefs have also come to a similar conclusion to mine. Not only have Moffat, Albrecht and Magueijo and others pointed out that the speed of light was significantly higher in the past, but Barrow has also suggested that it may still be continuing to change. This is a current, and open, field of research, and I encourage Day to read material more up to date than that which was published in the 1980's.
In the meantime, my work is still continuing on other aspects of the topic. In line with work done by Tifft, Van Flandern, Puthoff, Troitskii, and a number of other researchers, it appears that there is some solid evidence in space itself regarding the changing speed of light. This is the subject of a paper completed this year which has been submitted to a physics journal for peer review. Others from both evolution and creation backgrounds are also continuing research regarding the changing speed of light. As a result, c-decay is alive and well, and Robert Day's dismissal of the proposition appears to be somewhat premature. -- BARRY SETTERFIELD, August 2000.
Transcript of a UK Science Television Program (10/23/00)
Einstein's Biggest Blunder
Programme transcript
Dr Joao Magueijo: We did something which most people consider to be a bit of a heresy. We decided that the speed of light could change in space and time, and if that is true then our perceptions of physics will change dramatically.
Narrator: At the dawn of a new century, a new theory is being born. It threatens to demolish the foundations of 20th century physics. Its authors are two of the world's leading cosmologists. If they're right, Einstein was wrong. It all began when Andy Albrecht and Joao Magueijo met at a conference in America in 1996.
Prof Andy Albrecht: This was pretty, exciting. Most of the key people were there and there were lots of debates about the contemporary issues in cosmology. Joao came up to me late one evening and had a very interesting idea.
Dr Joao Magueijo: This is total bullshit! It wasn't like that at all.
Interviewer: Joao how do you remember it?
Dr Joao Magueijo: I remember there was this conversation between the three of us, and then each one of us suggested something. I remember I suggested the varying speed of light and there was embarrassed silence. I think you two thought I was taking the piss at this point.
Prof Andy Albrecht: Maybe, possibly but
Dr Joao Magueijo: But then, oh he's actually serious, he's not laughing; then we started taking it more seriously.
Narrator: For most scientists the idea that the speed of light can change is outrageous; it flatly contradicts Einstein's theories of space and time. But recently astronomers have begun to realize that the Universe doesn't always behave as his theories would lead you to expect.
Prof Andrew Lange: We're making measurements which indicate that the Universe is filled with some kind of energy density and we don't understand this energy at all. It's unlike anything else in physical theory.
Prof Richard Ellis: And the surprise is that instead of the Universe slowing down, in fact it's speeding up.
Prof John Webb: It's certainly a very profound result for physics because it will be the first ever indication that the laws of nature were not always the same as they are today.
Prof Richard Ellis: Who knows what's in store? I think in some way it's a very exciting time: it's very similar to the revolution that was seen in physics at the turn of the last century. So here we are about to enter the new millennium with a whole lot of uncertainties in store.
Narrator: To understand what's at stake, we need to go back to that scientific revolution. It began here in Bern Switzerland in 1905. As the new 20th century dawned, the intricate mechanism of 19th century physics was beginning to show signs of strain. It was finally demolished, not by an established scientist, but by a patent clerk.
Prof Dave Wark: When Einstein started his career, we still lived in a Newtonian clockwork Universe. Space and time were simply a reference system. The meter was a meter anywhere you went,and time clicked at a constant rate throughout the whole Universe. It was unaffected by where you were, whether you were moving or not.
Dr Ruth Durrer: Time was considered as an absolute concept - the time would be everywhere the same, independent of the state of motion of somebody. That there would exist an absolute time which could be measured with a clock. This was the concept which Einstein smashed with his new thought.
Narrator: The tool that Einstein used to shatter the clockwork Universe was the speed of light. He knew that for 20 years scientists had been puzzled by an experiment which suggested there was something decidedly odd about the speed of light. In the 1880s two American scientists, Albert Michelson and Edward Morley set out to measure how the speed of light was affected by the Earth's motion through space. They set up an experiment with beams of light.
Prof John Baldwin: In this experiment there's a light source which is the laser, and one's splitting the laser beam into two, sending them in two directions at right angles, and measuring in a sense the relative speed of light along those two beams and recombining them. The pattern that you see is the interference between two beams and it's measuring the relative speed of light within those two beams.
Narrator: If the apparatus were static there'd be no reason to expect a difference between the beams, but in fact it's moving very fast indeed. Our planet orbits the sun at 30 kilometers a second. It also spins around its axis once a day so every laboratory on Earth is spinning through space.
Prof John Baldwin: Well at this time of day the Earth is moving in this direction through space round the sun. If we then waited six hours, the Earth would have turned and then this direction would be the direction of motion of the Earth through space; then in another six hours this direction would be back but reversed. So that by doing nothing you can just sit here and very, very smoothly the Earth takes you round and then you can just look at the stability of your apparatus.
Narrator: Michelson and Morley assumed that the planet speed would add to the speed of the light beams and their apparatus. So they expected to see a regular pulsing of the pattern every six hours as the Earth's motion added to the speed of light in first one beam and then the other.
Prof John Baldwin: The surprising thing of course was that the measurements showed that nothing happened, and no matter how they did it and when they did it and whether they waited a long time, all year even, still nothing happened. And that's the beauty of the experiment that if you can measure nothing very, very precisely then you've got something really important.
Narrator: The importance of this result was that it proved that you can never add to or subtract from the speed of light. This was a direct contradiction to what was supposed to happen in the clockwork Universe. When space and time are fixed, speeds must always add up.
Prof Dave Wark: In such a world one has a very simple rule for the addition of speed, the addition of velocities. In Einstein's example, if you're walking along a tram or a train, your speed, with respect to the ground outside, is just the sum of your speed walking along the tram and the tram speed with respect to the ground.
Narrator: But the Michelson, Morley experiment had proved that this was not true for light. Light leaves the tram at the speed of light and strikes the pedestrians at the speed of light and this speed never changes, no matter how fast the tram is going. But something must change as a result of the tram speed. Einstein realized that it must be space and time themselves.
Dr Ruth Durrer: Once you assume that the speed of light is the fixed thing, this will imply that space and time can no longer be fixed and that, for example, a moving clock which is moving with respect to you goes slower.
Narrator: So, viewed from the pavement, the speed of the light from a tram is not affected by its motion. Instead the watch, as the passengers are waiting, will run slow compared to a stationary clock. In a small two-room apartment a few yards from the clock tower, Einstein wrote up his radical theory of Special Relativity.
Prof Dave Wark: Advertisement for the unemployed Einstein offering
Dr Ruth Durrer: ...private courses in mathematics and physics for students. For some time he was unemployed; nobody wanted him. They thought he was too lazy.
Prof Dave Wark: I think they thought he was too troublesome. Does it say there how much he charges?
Dr Ruth Durrer: It says that test lessons are free.
Prof Dave Wark: Ok, I think I'll come by and have a test lesson.
Narrator: But Einstein's fortunes were about to change.
Dr Ruth Durrer: So it's 1905, he's 26.
Narrator: In that year he published several papers of which Relativity was just one.
Dr Ruth Durrer: Six papers if you count the PhD dissertation.
Prof Dave Wark: In one year. And each one founds a field of physics.
Dr Ruth Durrer: And each one is worth the Nobel Prize.
Prof Dave Wark: I wonder if he'd realized just how big a change he was making to the world when he wrote that down.
Dr Ruth Durrer: And that's the E=mc2 paper, which he published very shortly after that one.
Prof Dave Wark: Look how thin it is! Jesus! Three pages - if I could trade all of my lifetime publications for these three pages!
Narrator: But Einstein himself was not satisfied. The problem was that his theory of relativity broke down when gravity entered the picture and gravity was the dominant force in the Universe. Einstein realized that he had to take his notion of flexible space and time even further.
Prof Dave Wark: He had to give space-time actual properties, it was no longer just in an empty place where things occur, it was something that actually was interactive. So in his famous statement, mass tells space how to curve, the presence of mass actually curves space-time.
Prof Dave Wark: And in the flip side of that, his next part of this statement is: space tells mass how to move, so a mass moving through space-time now just follows the curvature induced on it by the presence of a mass.
Prof Dave Wark: And this solved an old problem from Newtonian mechanics: the Earth is going round the sun. The Earth feels a gravitational attraction to the sun. How does it do that? How does the Earth know the sun is there? What is the source of this instantaneous action at a distance? In Einstein's model there is no such instantaneous action at a distance. The mass of the sun simply curves space-time and then the Earth follows that curve. Just like this tram follows the tram line it is on in response to the local curvature of the tracks; it doesn't know if those tracks are going to curve some distance in advance; it doesn't need to know. It just follows the local curvature of the track.
Prof Dave Wark: Einstein realized that it wouldn't just be mass that would cause gravity, it wouldn't just be mass that curved space time.
Dr Ruth Durrer: Every form of energy, like heat or also pressure, reacts to the gravitational field.
Prof Dave Wark: There's nuclear energy many, many different types of energy and all of them cause space-time to curve the same amount, depending just on the total amount of energy present. Mass is nothing special in this regard.
Narrator: For 10 years Einstein searched for an equation to express this relationship between mass-energy and space-time. In the end it was stunningly simple. G = 8 p T. In five characters the Einstein field equation encompasses the structure of the entire Universe. It ranks as one of the supreme achievements of human thought.
Dr Ruth Durrer: When, as a student, you learn this theory you find it extremely beautiful and simple. But then if you think: how did he get it? How on Earth did he find out these equations? That's a miracle.
Narrator: But Einstein didn't stop. He set out to use his new equations to describe the entire Universe. It was a bold leap and immediately he ran into problems - problems which still remain.
Dr Joao Magueijo: Relativity was a great success at least until Einstein had the courage to apply relativity to the Universe as a whole. He invented cosmology, scientific cosmology, but at the same time he gave us a lot of problems which are still with us. Basically, the Universe as we see it doesn't want to behave according to relativity.
Narrator: Einstein's approach was based on a daring assumption. He knew that locally stars would distort space-time in complicated ways that would be too difficult to calculate. But he believed that if he stepped back far enough, all the matter in the Universe would look like molecules in a cloud of gas.
Narrator: The cosmological fluid. From this perspective, the shape of space-time would be uniform and simple enough to deal with. But when he began to calculate how the Universe would behave under the influence of gravity he got a nasty shock.
Prof Dave Wark: You look out in the Universe and you see what appears to be relatively stable: the unchanging stars. And in Einstein's era they thought the Universe was remarkably static. It looked the same over time. But in Einstein's solutions this couldn't be true.
Narrator: Einstein found that his equation predicted that all the matter and energy in the Universe would fold space-time back upon itself. Soon the Universe would meet a fiery end as all the stars and galaxies collapsed into an enormous fireball.
Dave Wark: And in order to prevent this, Einstein had to add a term which he called the cosmological constant.
Narrator: To Einstein this extra term, lambda, the cosmological constant, spoilt the beauty of his original equation. But he could see no other way to make the Universe stable.
Prof Dave Wark: Now this is a constant that gives space-time itself the property that it would tend to spontaneously expand, and so he added that constant in just the right amount so that this property of space-time to expand would exactly balance the property of the matter in the galaxy or in the Universe to collapse under its own gravity. So by exactly balancing these two, he could therefore make the Universe stable. Now it wouldn't really have worked of course because it's the stability of a pencil on its point. Even the smallest deviation - too small a matter of density, too large amount of density - would have made the Universe collapse or expand, so I don't really think he'd solved the problem.
Narrator: Einstein's problem was that, according to his theory, the Universe was inherently unstable; it should have collapsed or exploded long ago. It's a mystery that worries scientists to this day.
Part 2
Narrator: This is the echo of creation. Detune a television set and it will pick up microwave radiation from the edge of the visible Universe. When it' set out on its journey, it was orange light but over the 15 billion years it has been traveling the Universe, it has grown a thousandfold, stretching the light so that we now see it as microwaves. It warms us as it warms the entire cosmos, raising the temperature of space by 3 degrees. This signal is powerful evidence that the Universe is not unchanging as Einstein imagined but that everything we see around us was once part of an immense fireball. The first hints of that fiery beginning were found when astronomers started to look out into space beyond our own galaxy.
Prof Richard Ellis: The 1920s was an exciting time in astronomy because that's when the first large telescopes came on line and Edwin Hubble, an American astronomer, started looking at nearby stellar systems which we now call galaxies.
TV voice: Dr Edwin Hubble on a movable platform lines up the massive telescope as he begins a cold night's work.
Prof Richard Ellis: And to his astonishment he found that they were very, very far away firstly, and secondly by measuring the light from these galaxies, he was able to see that they were moving away from us.
Narrator: To Hubble this could only mean one thing: the Universe itself must be expanding.
Prof Richard Ellis: It's a pretty profound discovery that the Universe is expanding because what that means is that at some point in the past, things were closer together. So if you measured density - the number of galaxies in a little box of space - then as you go back in time, the number that fit in a fixed box of space goes up and so the Universe becomes much denser and hotter. As one goes back in time, eventually you will come to a point which we call the Big Bang when the density was extremely high. And so the profundity of this discovery is that the Universe had a beginning: a Big Bang.
Narrator: If Hubble was right and the Universe had started with a cosmic explosion, then the force of this alone might be enough to counterbalance gravity's tendency to make the Universe collapse and die. Perhaps here was a way to make the Universe stable and solve Einstein's problem.
Prof Richard Ellis: You would have thought Einstein would respond positively to observations, but as is often the case, theorists completely ignore observations and so here was Hubble with a fantastic discovery - probably discovery of the century - and Einstein really didn't take any notice of it. So Einstein stuck to his static Universe, insisted on his cosmological constant to keep the Universe static, and it wasn't really until a meeting here in California between Hubble and Einstein in about 1932 that really there was a synergy between Einstein and the expanding Universe.
TV voice: And here he comes, down from the sun tower after a hard morning, looking a few million miles into his favorite space.
Narrator: Hubble, in the middle here, soon convinced Einstein that the Universe was indeed expanding. The cosmological constant which Einstein had introduced to hold up a static Universe against the force of gravity appeared to be unnecessary after all. With relief Einstein returned to the original form of his general theory of relativity.
Prof Richard Ellis: And it's at that time, or shortly after that, Einstein said that the invention of this cosmological constant was his biggest blunder.
TV voice: The construction is very was very skillful. You had to build up the outside and then put in the inside and then more outside and inside it was a great piece of engineering
Narrator: But Einstein's optimism was premature. It has gradually dawned on cosmologists that the Big Bang doesn't in fact solve the problem with the Universe stability. For 21st-century physicists like Joao Magueijo and Andy Albrecht, the cutting edge of research is still the problem first identified by Einstein back in 1916.
Prof Andy Albrecht: If we can really make that connection, then it's the reason why people should want the speed of light to vary.
Prof Andy Albrecht: You'd think, with all the great success of the Big Bang, we'd be happy, we wouldn't be complaining. But there's a problem with the Big Bang, and the problem is we shouldn't be here.
Narrator: The Universe has been gently expanding for 15 billion years. That's allowed time for stars, planets and cosmologists to evolve. The problem is, it's almost impossible to get a gently expanding Universe out of the Big Bang. Either it expands too fast or it falls back in on itself. Either way the Universe could not last very long.
Prof Andy Albrecht: A good analogy is to think about throwing a rock in the air. You throw it up; you expect it to come back after a little while. You throw a little bit harder and it goes further; but eventually comes back. If you throw it hard enough and no human can do this but NASA can do it with a space ship - you can leave the gravitational attraction of the Earth and fly off forever.
Prof Andy Albrecht: With the Universe there's this delicate balance. You throw the rock in the air it keeps going. Is it gonna turn around? You don't know, it keeps going, it keeps going, you don't see it flying off, you don't see it turning around, it's balanced right at the end for year after year, thousands of years, billions of years. We're now almost 15 billion years, we still don't know - is it coming back is it flying off? That's what the Universe is like.
Narrator: With the ball it's how fast you throw it. With the Universe the key thing is the amount of matter and energy in the Big Bang. To produce gentle expansion, the density of this energy has to be precisely right.
Prof Andy Albrecht: How do we start this Universe out in such a special state? We have to take a number that describes the density of the matter in the Universe and get it right to a hundred decimal places. One after the other, if we get one decimal place wrong the whole thing gets out of whack. No physicist can stomach setting up a Universe in such a delicate way.
Narrator: Yet something set up the Universe in the right way. Some mysterious process made sure that matter and energy had everywhere the same critical density keeping the entire cosmos in perfect balance.
Narrator: Scientists call this the flatness problem.
Dr Joao Magueijo: So this is the flatness problem: it's the fact that the Universe is a bit like a pencil standing on its stick for 15 billion years.
Narrator: And it's even worse than that.
Andy Albrecht: The puzzle is that when you start saying OK, suppose at the beginning things were different and something could come along and adjust everything just the way you need it, you run into the following problem: nothing can travel faster than the speed of light.
Narrator: The Universe is very, very big. Bigger than we can imagine and bigger than we can see. There are regions of space so far away they are invisible because the light from them has not yet had time to reach us. In effect we are surrounded by a horizon; this horizon has been growing at the speed of light since the Universe began but beyond it are regions with which we have never had any kind of contact. Since nothing, not energy nor any kind of physical process can travel faster than light, nothing can cross the horizon.
Dr Joao Magueijo: The Universe is now 15 billion years old which means that the horizon is actually very large. Nowadays it's about 30 billion light years across. This doesn't mean that the Universe is only this size; of course the Universe is infinite. It just means the region we can see is this 30 billion light year region, and when the Universe is very young, it's still very big but conversely you see a smaller and smaller fraction because the horizon is smaller and smaller.
Narrator: To see what this means, imagine that we could travel back in time. We would see the Universe shrinking rather than expanding, but our view of it would shrink even faster because our horizon would be shrinking at the fastest possible speed: the speed of light. Galaxies that are visible today would have been invisible to us in the past, and to each other. So the early Universe was divided up into small islands, isolated inside their own small horizons. This picture of a disconnected Universe flies directly in the face of the idea of a single balancing process needed to solve the flatness problem. Confused? So were the cosmologists. The only way round this horizon problem was to assume that the entire region we see today started out so tiny it would fit inside a single horizon. This idea, called inflation, was first proposed by Alan Guth and then developed by Paul Steinhardt and his colleague Andy Albrecht. Today, their version of inflation is widely accepted among scientists but Andy Albrecht himself has never been wholly convinced by his own theory.
Prof Andy Albrecht: What we have to do to make inflation work is invent an entirely new form of matter that exists in the early Universe and then disappears so we don't have it around today. And I was always left with the nagging feeling that if you invent so much, is inflation really the right thing to invent? Or could nature have chosen something else?
Narrator: As a young researcher at Cambridge in the mid-1990s, Joao Magueijo was also skeptical about inflation.
Dr Joao Magueijo: Because inflation is the only thing available, people cling to it, just like to a lifeboat. To be a bit extreme, you could say, you could solve all these fine-tuning problems using divine intervention and I think inflation is a scientifically acceptable way to invoke divine intervention at some point.
Prof Andy Albrecht: I think that's a bit over the top but there's enough open questions that we really need to think about it.
Narrator: One day Joao saw that there might be a much simpler way to solve the horizon problem.
Dr Joao Magueijo: I realized that if you were to break one single but sacred rule of the game, the constancy of the speed of light, you could actually solve the horizon problem. And when you think back on it, it's just such an obvious thing that when Universe is very young if the light was very fast you could have a very large horizon. When the Universe was one year old the horizon would be one quick light here across to here, which could be as big as you wanted and of course you can connect the whole of your Universe if you do this.
Narrator: If early light was much faster, a single horizon could be big enough to encompass the entire known Universe. It was a bold idea, too bold.
Dr Joao Magueijo: This came at the time when I was a fellow of this college but it was also a stage in my career where I had to look for a job, I was about to finish my position here - not the time to go and pursue a very original idea. I was already quite controversial. I didn't need another thing that would be even more controversial. There were times when I saw myself selling the Big Issue outside St John's College! So I waited until I was on much safer ground.
Narrator: Joao found that safer ground when the Royal Society awarded him a rare and prestigious research fellowship. He joined Andy Albrecht's group at Imperial College. They started to work on Joao's idea together.
Dr Joao Magueijo: One day Andy just called me to his office and he said, 'Joao let's work on the varying speed of light here,' and he closed the door and made a big secret about it. He cleaned the blackboard afterwards; he was really afraid someone might steal the idea. Then gradually we just started putting more and more material together, trying to find more and more things about the theory.
Prof Andy Albrecht: You face the frontier, you face unknown questions and you argue about it and you have competing ideas and, after a while one is clearly the winner.
Dr Joao Magueijo: And you're really worried about something, it really is with you all the time, not just in your office. You go through phases in which you dream about your ideas, you sleep over your ideas you wake up tired. Well you need to cast things into equations in the end because this is what science is all about. It's about mathematical models not just theories, otherwise it's all very cranky. I think there is a very unique aspect of scientific discovery, there is a big adrenaline rush when you've spent months and months struggling with the problem getting it wrong and eventually you discover something and it's unique. I'm addicted to adrenaline in general but this one is unique.
Narrator: Joao and Andy were creating a completely new physics. As they explored this strange new world it began to dawn that perhaps they could solve more than just the horizon problem.
Dr Joao Magueijo: We got more than what we bargained for and this is really where the thing was massively rewarding. We found that we could solve the flatness problem as well and the reason for that is we realized very quickly there's no way we have energy conservation if the speed of light varies.
Narrator: In conventional physics, energy is conserved. It can be transformed but it cannot be created or destroyed. This is the principle of the conservation of energy and it means that the total amount of energy in the Universe is fixed. So the critical energy density the Universe needs must be established perfectly, right from the beginning.
Dr Joao Magueijo: Now if we change something as fundamental as the speed of light, which is woven into the whole fabric of physics, then of course you're breaking that principle: the Universe is different at different times. And you don't conserve energy. But then you realize this is exactly what you need to solve the flatness problem because you violate energy conservation pushing the Universe to the critical energy density. That is, you create energy if you have sub-critical energy density and vice versa. You take away energy if you have a surplus of energy density.
Narrator: In their theory, during the early Universe the speed of light was falling, which allowed the cosmos a built-in thermostat, creating or destroying energy so that the critical density was maintained exactly. Thus the Universe remained in balance for billions of years.
Dr Joao Magueijo: We were just trying to find an alternative to inflation as far as the horizon problem was concerned. We actually did not have hopes of solving everything. This was a gift we got out of it.
Narrator: Joao and Andy had set out to solve the horizon problem and stumbled upon a theory that solved the puzzle which had plagued cosmology since the time of Einstein. They had made a Universe that was inherently stable, held in balance by the creation or destruction of energy. A theory which predicted the Universe as we see it today. However it was still just a theory; proof could only come from the depths of space-time. But what astronomers found there would astonish everyone. Suggesting that the speed of light was also the key to the biggest mystery in cosmology: what happened before the Big Bang.
Part 3
Narrator: Long ago when the Universe was young, light itself traveled faster than it does today. The laws of physics were very different; that at least was the theory. The evidence could only come from the world's great telescopes. As they scan the far depths of space, astronomers also look back in time.
Narrator: In 1998 the British astronomer John Webb started to become interested in the question of whether the fundamental constants of nature could change as the Universe evolved.
Prof John Webb: We're using a technique which enables us to look back into the past to measure physics as it was a long time ago. So we're doing that using quasars.
Narrator: Quasars are the most distant objects we can see; they are thought to be primitive galaxies in the process of formation. But John Webb is not interested in the quasars themselves.
Prof John Webb: Quasars are just, as far as we're concerned for this study, very distant sources of light which shine through the Universe to us. In doing so, they intersect gas clouds along the line of sight and then we can study the physics of those gas clouds by looking at the way in which the light is absorbed. We can look at gas clouds relatively nearby, and we can look at them just about as far away as the most distant quasars. That means in terms of looking back in time almost 10 billion years, or something like that, an awful long time ago. So we're studying physics as it was when the Universe was quite young.
Narrator: When light passes through an interstellar gas cloud it collides with the electrons and the gas molecules. This creates a pattern of dark lines in its spectrum. What John Webb noticed was that this pattern looked different in the spectra from the most distant clouds. The inference was astonishing: either the electrons were different or the speed of light was greater in the distant past.
Prof John Webb: If it's correct, it's certainly a very profound result for physics because it would be the first ever indication that the laws of nature were not always the same as they are today.
Narrator: But far off in space and time an even more amazing discovery was waiting for astronomers: today cosmology is buzzing with news of the unexpected comeback of an idea discarded 70 years ago. Einstein's cosmological constant, lambda.
Narrator: For Joao it means taking his theory even further. He now believes the cosmological constant could be the link that connects changes in the speed of light to the origin of the Universe itself.
Dr Joao Magueijo: So Einstein has already endowed space-time with its own life, when he allowed space-time to curve, to have its own dynamics - and the cosmological constant was one step further - it was basically giving space-time its own energy so that even before he put matter into space-time, when we have vacuum, you have some energy density in this vacuum and this is what lambda is, and it has this very interesting property that essentially it makes repulsive gravity.
Narrator: Lambda produces gravity that pushes things apart rather than pulling them together and that seems to be what's happening to the Universe, something is blowing it apart.
Narrator: Ever since Hubble convinced Einstein that the Universe is growing, astronomers have been trying to measure its rate of expansion. The breakthrough came when they started to concentrate on exploding stars called supernovae. They thought that these would allow them to chart the gentle deceleration of the Universe. What they actually found was precisely the reverse.
Prof Richard Ellis: Now the question is, is the Universe slowing down as we would expect? The surprise is that instead of the Universe slowing down, in fact it's speeding up.
Narrator: Something is upsetting the delicate balance of the Universe, pushing the galaxies apart faster and faster. A new force in the vacuum of space.
Prof Richard Ellis: The acceleration as seen from the supernova data, of course, raises the amazing question of resurrecting Einstein's cosmological constant.
Narrator: It looks as if space-time is humming with energy. Buried in the equations of this theory, Joao has found a hidden link between this energy and the speed of light.
Dr Joao Magueijo: Well at some point we've found out two interesting things. One was that the energy in the cosmological constant also depends on the speed of light, and in particular if the speed of light drops, then the energy in the vacuum drops as well. And the second thing we've found is that this cosmological constant itself promotes changes in the speed of light - it can make it drop in value. So we have an instability.
Narrator: In Joao's theory, a change in the vacuum can cause a drop in the speed of light, but this in turn reduces the amount of energy the vacuum can hold, forcing energy out of it and into ordinary matter and radiation. Could this be the genius of the Universe? What happened before the Big Bang?
Dr Joao Magueijo: So in some of these scenarios in the beginning there is just a vacuum - but the vacuum is not nothing, it's actually the cosmological constant, this pull of energy in the vacuum. And in these theories, it is this energy that drives changes in the speed of light; it makes a drop in value. And what that does is that makes all the energy in the cosmological constant drop as well. It has to go somewhere. Where does it go? It goes into all the matter of the Universe, so it caused a Big Bang. So in this scenario it's actually this sudden drop in the speed of light - this change in the speed of light - that causes the Big Bang.
Narrator: In the beginning was the void. But the void was not nothing and there was light and the light changed. And so the void brought forth the world and the world was good, for it endured until men could comprehend it. But it will come to pass that one day the energy of the void will have pushed all things away, leaving nothing but the void. But the void is not nothing.
Dr Joao Magueijo: And you might think this is the end of the Universe, but of course in the picture of this theory it's just creating the conditions for another Big Bang to happen again - a sudden drop in the speed of light, another sudden discharge of all this energy into another Big Bang. So it is possible that actually our Big Bang is just one of many, one of many yet to come, and one of many which there were in the past already - maybe the Universe is just this sequence of Big Bangs all the time.
Narrator: Joao's bold challenge to the constancy of the speed of light has led him to a wholly new view of the cosmos. One in which the Universe no longer has a beginning and an end, but is eternal. An endless cycle of Big Bangs drawn from the vast reservoir of energy in the vacuum. And like every cosmologist before him, Joao has been guided by the theory that started it all: it is a measure of Einstein's genius that even when he was wrong, somehow he was right. What he called his biggest blunder may yet prove his greatest legacy.
Joao Magueijo: Well of course I respect relativity enormously and I have this feeling that it is only now that I have contradicted relativity that I really understand it. And it's actually just because I've gone against it that I'm showing my full respect to the great man. This is not at all trying to contradict Einstein, it's just trying to take things one step further. Eventually of course it will be nature that will decide whether this is true or not. I'm working on trying to find ways of deciding whether the theory is right or wrong. Some kind of experiment which will decide conclusively whether the varying speed of light theory is pure nonsense or not.
Question: I'm not a scientist, although I have some math and science background, and I am only just beginning to look into this discussion and may be asking a stupid question. Apology stated. I am a fellow believer and view Genesis as the ultimate "Theory" for which we need to find proof (not that we need to defend God, but it seems a reasonable part of our witness). That said, I want to review the emerging theories somewhat objectively. I noticed in Setterfield's paper there was reference to conservation of energy E=MC2. I found it interesting that VSL theory put forth by Magueijo doesn't require that, but seems to say energy will not be conserved with time. Have Setterfield (or yourself) reviewed the work of Magueijo? Perhaps he has discovered something important. Ultimately any theory has to make since on an earth populated by humans to be of any use to us. Does this consideration require conservation of energy in the Setterfield theory? Or, is it possible that energy may not be conserved over the history of the universe?
Response: Yes, we certainly have considered Albrecht and Magueijo's paper and are aware of what he is proposing. His paper is basically theoretical and has very little observational backing for it. By contrast, my papers are strictly based on observational evidence. This requires that there is conservation of energy. The observational basis for these proposals also reveals that there is a series of energy jumps occurring at discrete intervals throughout time as more energy becomes available to the atom. Importantly, it should be noted that this energy was initially invested in the vacuum during its expansion, and has become progressively available as the tension in the fabric of space has relaxed over time thus converting potential energy into the kinetic energy utilized by the atom. The atom can only access this energy once a certain threshold has been reached, and hence it occurs in a series of jumps. This has given rise to the quantized redshift that occurs in space.
Thus observational evidence agrees with the conservation approach rather than Mageuijo's approach. Barry. 1/31/01.
Question: I emailed you about this topic a year or two ago, and I've since taken a class in radioisotope chemistry at UCI. As a result I was using some of my texts to examine the decay of Americium 241 and noted the naturally occurring decay chains for U235, U238 and Th232, as well as the fully decayed chain for Pu241. My thought is, can the relative natural abundances of these chains' terminal products (Pb208,207, and 206) be used to calculate an initial abundance and time frame for the original atomic abundances of the parent isotopes which could be compared to the predictions of Willie Fowler regarding stellar nucleogenesis processes. I hope to hear from you soon! Thanks again for all your interesting and informative web postings and work.
Response: I believe that it is possible to determine the initial ratios of the parent elements in the various chains. It is through this mechanism that the radiometric age of the universe is usually calculated as being on the order of ten billion years. Professor Fowler did exactly this and has maintained his calculated radiometric age for the universe at about 10 billion years, with which I am basically in agreement. Interestingly, using these sorts of ratios, one piece of moon rock dated as being 8.2 billion years old, to the amazement of the dating laboratory involved.
As far as stars are concerned, the Th/Nd ratio has been shown to be unchanged no matter what the age of the star is, which leads one to two conclusions. Firstly, supernovae have not added a significant amount of new elements to putative star-forming clouds. If they had, the ratio would be different in various stars. This then suggests that the majority of the elements were formed at the beginning rather than through a series of supernovae explosions.
Given that point, it seems that the stars must be basically the same age. BARRY, 1/30/01.
Question from a university astronomy professor: Barry points out that for obvious reasons no change in the speed of light has been noticed since the redefinition of time in terms of the speed of light a few decades ago. However, the new definition of time should cause a noticeable drift from ephemeris time due to the alleged changing speed of light. I'm not aware of any such drift. Ephemeris time should be independent of the speed of light. Before atomic standards were adopted, crystal clocks had documented the irregular difference between ephemeris time and time defined by the rotation of the earth. Has Barry investigated this?
Response: On the thesis being presented here, the run-rate of atomic clocks is proportional to 'c'. In other words, when 'c' was higher, atomic clocks ticked more rapidly. By contrast, it can be shown that dynamical, orbital or ephemeris time is independent of 'c' and so is not affected by the 'c' decay process. Kovalevsky has pointed out that if the two clock rates were different, "then Planck's constant as well as atomic frequencies would drift" [J. Kovalevsky, Metrologia 1:4 (1965), 169].
Such changes have been noted. At the same time as 'c' was measured as decreasing, there was a steady increase in the measured value of Planck's constant, 'h', as outlined in the 1987 Report by Norman and Setterfield. However, the measured value of 'hc' has been shown to be constant throughout astronomical time. Therefore it must be concluded from these measurements that 'h' is proportional to 1/c precisely. As far as different clock rates is concerned, the data is also important. During the interval 1955 to 1981 Van Flandern examined data from lunar laser ranging using atomic clocks and compared them with dynamical data. He concluded that: "the number of atomic seconds in a dynamical interval is becoming fewer. Presumably, if the result has any generality to it, this means that atomic phenomena are slowing down with respect to dynamical phenomena" [T. C. Van Flandern, in 'Precision Measurements and Fundamental Constants II,' (B. N. Taylor and W. D. Phillips, Eds.), NBS (US), Special Publication 617 (1984), 625]. These results establish the general principle being outlined here. Van Flandern also made one further point as a consequence of these results. He stated that "Assumptions such as the constancy of the velocity of light may be true only in one set of units (atomic or dynamical), but not the other" [op. cit.]. This is the kernel of what has already been said above. Since the run-rate of the atomic clock is proportional to 'c', it becomes apparent that 'c' will always be a constant in terms of atomic time. Van Flandern's measurements, coupled with the measured behavior of 'c', and other associated 'constants', indicate that the decay rate of 'c' was flattening out to a minimum which seemed to be attained around 1980. Whether or not this is the final minimum is a matter for decision by future measurements. But let me explain the situation this way. The astronomical, geological, and archaeological data indicate that there is a ripple or oscillation associated with the main decay pattern for 'c'. In many physical systems, the complete response to the processes acting comprises two parts: the particular or forced response, and the complimentary, free, or natural response. The forced response gives the main decay pattern, while the free response often gives an oscillation or ripple superimposed on the main pattern. The decay in 'c' is behaving in a very similar way to these classical systems.
There are three scenarios currently undergoing analysis. One is similar to that depicted by E. A. Karlow in American Journal of Physics 62:7 (1994), 634, where there is a ripple on the decay pattern that results in "flat points", following which the drop is resumed. The second and third scenarios are both presented by J. J. D'Azzo and C. H. Houpis "Feedback Control System Analysis and Synthesis" International Student Edition, p.258, McGraw-Hill Kogakusha, 1966. In Fig. 8-5 one option is that the decay with its ripple may bottom out abruptly and stay constant thereafter. The other is that oscillation may continue with a slight rise in the value of the quantity after each of the minima. Note that for 'c' behavior, the inverse of the curves in Fig. 8-5 is required. All three options describe the behavior of 'c' rather well up to this juncture. However, further observations are needed to finally settle which sort of curve is being followed. (Barry Setterfield March 26, 2001).
Cosmic Dark Energy?
DISCREPANT REDSHIFTS
There has been much interest generated in the press lately over the analysis by Dr. Adam G. Riess and Dr. Peter E. Nugent of the decay curve of the distant supernova designated as SN 1997ff. In fact, over the last two years, a total of four supernovae have led to the current state of excitement. The reason for the surge of interest is the distances that these supernovae are found to be when compared with their redshift, z. According to the majority of astronomical opinion, the relationship between an object's distance and its redshift should be a smooth function. Thus, given a redshift value, the distance of an object can be reasonably estimated.
One way to check this is to measure the apparent brightness of an object whose intrinsic luminosity is known. Then, since brightness falls off by the inverse square of the distance, the actual distance can be determined. For very distant objects something of exceptional brightness is needed. There are such objects that can be used as 'standard candles', namely supernovae of Type Ia. They have a distinctive decay curve for their luminosity after the supernova explosion, which allows them to be distinguished from other supernovae.
In this way, the following four supernovae have been examined as a result of photos taken by the Hubble Space Telescope. SN 1997ff at z = 1.7; SN 1997fg at z = 0.95; SN 1998ef at z = 1.2; and SN 1999fv also at z = 1.2. The higher the redshift z, the more distant the object should be. Two years ago, the supernovae at z = 0.95 and z = 1.2 attracted attention because they were FAINTER and hence further away than expected. This led cosmologists to state that Einstein's Cosmological Constant must be operating to expand the cosmos faster than its steady expansion from the Big Bang. Now the object SN 1997ff, the most distant of the four, turns out to be BRIGHTER than expected for its redshift value. This interesting turn of events has elicited the following comments from Adrian Cho in New Scientist for 7 April, 2001, page 6 in an article entitled "What's the big rush?"
"Two years ago, two teams of astronomers reported that distant stellar explosions known as type Ia supernovae, which always have the same brightness, appeared about 25 per cent dimmer from Earth than expected from their red shifts. That implied that the expansion of the Universe has accelerated. This is because the supernovae were further away than they ought to have been if the Universe had been expanding at a steady rate for the billions of years since the stars exploded. But some researchers have argued that other phenomena might dim distant supernovae. Intergalactic dust might soak up their light, or type Ia supernovae from billions of years ago might not conform to the same standard brightness they do today."
"This week's supernova finding seems to have dealt a severe blow to these [alternative] arguments [and supports] an accelerating Universe. The new supernova's red shift implies it is 11 billion light years away, but it is roughly twice as bright as it should be. Hence it must be significantly closer than it would be had the Universe expanded steadily. Neither dust nor changes in supernova brightness can easily explain the brightness of the explosion."
"Dark energy [the action of the Cosmological Constant, which acts in reverse to gravity] can, however. When the Universe was only a few billion years old, galaxies were closer together and the pull of their gravity was strong enough to overcome the push of dark energy and slow the expansion. A supernova that exploded during this period would thus be closer than its red shift suggests. Only after the galaxies grew farther apart did dark energy take over and make the Universe expand faster. So astronomers should see acceleration change to deceleration as they look farther back in time. "This transition from accelerating to decelerating is really the smoking gun for some sort of dark energy," Riess says."
Well, that is one option. Interestingly, there is another option well supported by other observational evidence. For the last two decades, astronomer William Tifft of Arizona has pointed out repeatedly that the redshift is not a smooth function at all but is, in fact, going in "jumps", or is quantized. In other words, it proceeds in a steps and stairs fashion. Tifft's analyses were disputed, so in 1992 Guthrie and Napier did a study to disprove the matter. They ended up agreeing with Tifft. The results of that study were themselves disputed, so Guthrie and Napier conducted an exhaustive analysis on a whole new batch of objects. Again, the conclusions confirmed Tifft's contention. The quantizations of the redshift that were noted in these studies were on a relatively small scale, but analysis revealed a basic quantization that was at the root of the effect, of which the others were simply higher multiples. However, this was sufficient to indicate that the redshift was probably not a smooth function at all. If these results were accepted, then the whole interpretation of the redshift, namely that it represented the expansion of the cosmos by a Doppler effect on light waves, was called into question. This becomes apparent since there was no good reason why that expansion should go in a series of jumps, anymore than cars on a highway should travel only in multiples of 5 kilometers per hour.
In 1990, Burbidge and Hewitt reviewed the observational history of preferred redshifts for extremely distant objects. Here the quantization or periodicity was on a significantly larger scale. Objects were clumping together in preferred redshifts across the whole sky. These redshifts were listed as z = 0.061, 0.30, 0.60, 0.96, 1.41 and 1.96 [G. Burbidge and A. Hewitt, Astrophysical Journal, vol. 359 (1990), L33]. In 1992, Duari et al. examined 2164 objects with redshifts ranging out as far as z = 4.43 in a statistical analysis [Astrophysical Journal, vol. 384 (1992), 35]. Their analysis eliminated some suspected periodicities as not statistically significant. Only two candidates were left, with one being mathematically precise at a confidence interval exceeding 99% in four tests over the entire range. Their derived formula confirmed the redshift peaks of Burbidge and Hewitt as follows: z = 0.29, 0.59, 0.96, 1.42, 1.98. When their Figure 4 is examined, the redshift peaks are seen to have a width of about z = 0.0133.
A straightforward interpretation of this periodicity is that the redshift itself is going in a predictable series of steps and stairs on a large as well as a small scale. This is giving rise to the apparent clumping of objects at preferred redshifts. The reason is that on the flat portions of the steps and stairs pattern, the redshift remains essentially constant over a large distance, so many objects appear to be at the same redshift. By contrast, on the rapidly rising part of the pattern, the redshift changes dramatically over a short distance, and so relatively few objects will be at any given redshift in that portion of the pattern. From the Duari et al. analysis the steps and stairs pattern of the redshift seems to be flat for about z = 0.0133, and then climbs steeply to the next step.
These considerations are important in the current context. As noted above by Reiss, the objects at z = 0.95 and 1.2 are systematically faint for their assumed redshift distance. By contrast, the object at z = 1.7 is unusually bright for its assumed redshift distance. Notice that the object at z = 0.95 is at the middle of the flat part of the step according to the redshift analyses, while z = 1.2 is right at the back of the step, just before the steep climb. Consequently for their redshift value, they will be further away in distance than expected, and will therefore appear fainter. By contrast, the object at 1.7 is on the steeply rising part of the pattern. Because the redshift is changing rapidly over a very short distance astronomically speaking, the object will be assumed to be further away than it actually is and will thus appear to be brighter than expected.
These recent results therefore verify the existence of the redshift periodicities noted by Burbidge and Hewitt and statistically confirmed by Duari et al. They also verify the fact that redshift behavior is not a smooth function, but rather goes in a steps and stairs pattern. If this is accepted, it means that the redshift is not a measure of universal expansion, but must have some other interpretation.
The research that has been conducted on the changing speed of light over the last 10 years has been able to replicate both the basic quantization picked up by Tifft, and the large-scale periodicities that are in evidence here. On this research, the redshift and light-speed are related effects that mutually derive from changing vacuum conditions. The evidence suggests that the vacuum zero-point energy (ZPE) is increasing as a result of initial expansion of the cosmos. It has been shown by Puthoff [Physical Review D 35:10 (1987), 3266] that the ZPE is maintaining all atomic structures throughout the universe. Therefore, as the ZPE increases, the energy available to maintain atomic orbits increases. Once a quantum threshold has been reached, every atom in the cosmos will assume a higher energy state for a given orbit and so the light emitted from those atoms will be bluer than those in the past. Therefore as we look back to distant galaxies, the light emitted from them will appear redder in quantized steps. At the same time, since the speed of light is dependent upon vacuum conditions, it can be shown that a smoothly increasing ZPE will result in a smoothly decreasing light-speed. Although the changing ZPE can be shown to be the result of the initial expansion of the cosmos, the fact that the quantized effects are not "smeared out" also indicate that the cosmos is now static, just as Narliker and Arp have demonstrated [Astrophysical Journal vol. 405 (1993), 51]. In view of the dilemma that confronts astronomers with these supernovae, these alternative explanations may be worth serious examination.
BARRY SETTERFIELD, April 11, 2001
Thanks for forwarding the correspondence on the light-speed topic. Several points need be made. First this following statement reveals that your correspondent has yet to come up to date with some of the basics of the proposition. He wrote:
There are well-defined relationships in physics between wave speed, frequency, and wavelength as well as distance, velocity, and time. These are the relationships used by astronomers in defining the redshift. I demonstrate in detail how they inter-relate if the wave speed changes and at 3.75 million c, the frequency change would correspond to a z of 3,750,000-1 = 3,749,999 (equation 43). This follows straightforward from those definitions. To get Setterfield's results, millions of wave-crests must have just vanished on their way to Earth. If so, how?
In order to overcome this deficiency, the following technical notes give the foundation of that part of the proposition. As will be discovered upon reading this document, no wave-crests will disappear at all on their way to earth, and the energy of any given photon remains unchanged in transit. Not only does this follow from the usual definitions, but it is also gives results in accord with observation. This model maintains that wavelengths remain unchanged and frequency alters as Light speed drops. In order to see what is happening, consider a wave train of 100 crests associated with a photon. Let us assume that those 100 crests pass an observer at the point of emission in 1 second. Now assume that the speed of light drops to 1/10th of its initial speed in transit, so that at the point of final observation it takes 10 seconds for all 100 crests to pass. The number of crests has not altered; they are simply traveling more slowly. Since frequency is defined as the number of crests per second, both the frequency and light-speed have dropped to 1/10th of their original value, but there has been no change in the wavelength or the number of crests in the wave-train. The frequency is a direct result of light-speed, and nothing else happens to the wave-train.
Second, the standard redshift/distance relationship is not changed in this model. However, the paper demonstrates that there is a direct relationship between redshift and light-speed. Furthermore, astronomical distance and dynamical time are linearly related. As a consequence, the standard redshift/distance relationship is equivalent to the relationship between light-speed and time. The graph is the same; only the axes have been re-scaled.
As far as the redshift, z, is concerned, the most basic definition of all is that z equals the observed change in emitted wavelength divided by the laboratory standard for that wavelength. The model shows that there will be a specified change in emitted wavelength at each quantum jump that results in a progressive, quantized redshift as we look back to progressively more distant objects. This does not change the redshift/distance relationship or the definition of redshift. What this model does do is to predict the size of the redshift quantization, and links that with a change in light-speed. The maths are all in place for that.
I trust that this answers the main parts of the problem for your correspondent. Barry, September 21, 2001.
Technical Note:
A question has been asked about the behavior of the energy E of emitted photons of wavelength W and frequency f during their transit across space. The key formulas involved are E = hf = hc/W. The following discussion concentrates on the behavior of individual terms in these equations.
If c does indeed vary, inevitably some atomic constants must change, but which? Our theories should be governed by the observational evidence. This evidence has been supplied by 20th century physics and astronomy. One key observation that directs the discussion was noted by R. T. Birge in Nature 134:771, 1934. At that time c was measured as declining, but there were no changes noted in the wavelengths of light in apparatus that should detect it. Birge commented: "If the value of c is actually changing with time, but the value of [wavelength] in terms of the standard meter shows no corresponding change, then it necessarily follows that the value of every atomic frequency must be changing." This follows since light speed, c, equals frequency, f, multiplied by wavelength W. That is to say c = fW. If wavelengths W are unchanged in this process, then frequencies f must be proportional to c.
Since atomic frequencies govern the rate at which atomic clocks tick, this result effectively means that atomic clocks tick in time with c. By contrast, orbital clocks tick at a constant rate. J. Kovalevsky noted the logical consequence of this situation in Metrologia Vol. 1, No. 4, 1965. He stated that if the two clock rates were different "then Planck's constant as well as atomic frequencies would drift." The observational evidence suggests that these two clocks do indeed run at different rates, and that Planck's constant is also changing. The evidence concerning clock rates comes from the work of T. C. Van Flandern, then of the US Naval Observatory in Washington. He had examined lunar and planetary orbital periods and compared them with atomic clocks data for the period 1955-1981. Assessing the data in 1984, he noted the enigma in Precision Measurements and Fundamental Constants II, NBS Special Publication 617, pp. 625-627. In that National Bureau of Standards publication, Van Flandern stated "the number of atomic seconds in a dynamical interval is becoming fewer. Presumably, if the result has any generality to it, this means that atomic phenomena are slowing down with respect to dynamical phenomena."
To back up this proposition, Planck's constant, h, has been measured as increasing throughout 20th century. In all, there are 45 determinations by 8 methods. When the data were presented to a scientific journal, one Reviewer who favored constant quantities noted, "Instrumental resolution may in part explain the trend in the figures, but I admit that such an explanation does not appear to be quantitatively adequate." Additional data came from experiments by Bahcall and Salpeter, Baum and Florentin-Nielsen, as well as Solheim et al. They have each proved that the quantity 'hc' or Planck's constant multiplied by light-speed is in fact a constant astronomically. There is only one conclusion that can be drawn that is in accord with all these data. Since c has been measured as decreasing, and h has been measured as increasing during the same period, and hc is in fact constant, then h must vary precisely as 1/c at all times. This result also agrees with the conclusions reached by Birge and Kovalevsky.
From this observational evidence, it follows in the original equation E = hf = hc/W, that since f is proportional to c, and h is proportional to 1/c, then photon energies in transit are unchanged from the moment of emission. This also follows in the second half of the equation since hc is invariant, and W is also unchanged according to observation. Thus, if each photon is considered to be made up of a wave-train, the number of waves in that wave-train remains unchanged during transit, as does the wavelength. However, since the wave-train is traveling more slowly as c drops, the number of wave-crests passing a given point per unit time is fewer, proportional to c. Since the frequency of a wave is also defined as the number of crests passing a given point, this means that frequency is also proportional to c with no changes in the wave structure of the photon at all. Furthermore, the photon energy is unchanged in transit.
Barry Setterfield, September 14th 2001.
A genuine redshift anomaly seems to exist, one that would cause a re-think about cosmological issues if the data are accepted. Let's look at this for just a moment. As we look out into space, the light from galaxies is shifted towards the red end of the spectrum. The further out we look, the redder the light becomes. The measure of this red shifting of light is given by the quantity z, which is defined as the change in wavelength of a given spectral line divided by the laboratory standard wavelength for that same spectral line. Each atom has its own characteristic set of spectral lines, so we know when that characteristic set of lines is shifted further down towards the red end of the spectrum. This much was noted in the early 1920's. Around 1929, Hubble noted that the more distant the galaxy was, the greater was the value of the redshift, z. Thus was born the redshift/distance relationship. It came to be accepted as a working hypothesis that z might be a kind of Doppler shift of light because of universal expansion. In the same way that the siren of a police car drops in pitch when it races away from you, so it was reasoned that the red shifting of light might represent the distant galaxies racing away from us with greater velocities the further out they were. The pure number z, then was multiplied by the value of light speed in order to change z to a velocity. However, Hubble was discontent with this interpretation. Even as recently as the mid 1960's Paul Couderc of the Paris Observatory expressed misgivings about the situation and mentioned that a number of astronomers felt likewise. In other words, accepting z as a pure number was one thing; expressing it as a measure of universal expansion was something else.
It is at this point that Tifft's work enters the discussion. In 1976, Tifft started examining redshift values. The data indicated that the redshift, z, was not a smooth function but went in a series of jumps. Between successive jumps the redshift remained fixed at the value attained at the last jump. The editor of the Astrophysical Journal who published the first article by Tifft, made a comment in a footnote to the effect that they did not like the idea, but referees could find no basic flaw in the presentation, so publication was reluctantly agreed to. Further data came in supporting z quantization, but the astronomical community could not generally accept the data because the prevailing interpretation of z was that it represented universal expansion, and it would be difficult to find a reason for that expansion to occur in "jumps". In 1981 the extensive Fisher-Tully redshift survey was published, and the redshifts were not clustered in the way that Tifft had suggested. But an important development occurred in 1984 when Cocke pointed out that the motion of the Sun and solar system through space had a genuine Doppler shift that added to or subtracted from every redshift in the sky. Cocke pointed out that when this true Doppler effect was removed from the Fisher-Tully observations, there were redshift "jumps" or quantizations globally across the whole sky, and this from data that had not been collected by Tifft. In the early 1990's Bruce Guthrie and William Napier of Edinburgh Observatory specifically set out to disprove redshift quantization using the best enlarged example of accurate hydrogen line redshifts. Instead of disproving the z quantization proposal, Guthrie and Napier ended up in confirming it. The quantization was supported by a Fourier analysis and the results published around 1995. The published graph showed over 60 successive peaks and troughs of precise redshift quantizations. There could be no doubt about the results. Comments were made in New Scientist, Scientific American and a number of other lesser publications, but generally, the astronomical community treated the results with silence.
If redshifts come from an expanding cosmos, the measurements should be distributed smoothly like the velocity of cars on a highway. The quantized redshifts are similar to every car traveling at some multiple of 5 miles per hour. Because the cosmos cannot be expanding in jumps, the conclusion to be drawn from the data is that the cosmos is not expanding, nor are galaxies racing away from each other. Indeed, at the Tucson Conference on Quantization in April of 1996, the comment was made that "[in] the inner parts of the Virgo cluster [of galaxies], deeper in the potential well, [galaxies] were moving fast enough to wash out the quantization." In other words, the genuine motion of galaxies destroys the quantization effect, so the quantized redshift it is not due to motion, and hence not to an expanding universe. This implies that the cosmos is now static after initial expansion. Interestingly, there are about a dozen references in the Scriptures which talk about the heavens being created and then stretched out. Importantly, in every case except one, the tense of the verb indicated that the "stretching out" process was completed in the past. This is in line with the conclusion to be drawn from the quantized redshift. Furthermore, the variable light speed (Vc) model of the cosmos gives an explanation for these results, and can theoretically predict the size of the quantizations to within a fraction of a kilometer per second of that actually observed. This seems to indicate that a genuine effect is being dealt with here.
It is never good science to ignore anomalous data or to eliminate a conclusion because of some presupposition. Sir Henry Dale, one time President of the Royal Society of London, made an important comment in his retirement speech. It was reported in Scientific Australian for January 1980, p.4. Sir Henry said: "Science should not tolerate any lapse of precision, or neglect any anomaly, but give Nature's answers to the world humbly and with courage." To do so may not place one in the mainstream of modern science, but at least we will be searching for truth and moving ahead rather than maintaining the scientific status quo.
One basis on which Guthrie and Napier's conclusions have been questions and/or rejected concerns the reputed "small" size of the data set. It has been said that if the size of the data set is increased, the anomaly will disappear. Interestingly, the complete data set used by Guthrie and Napier set comprised 399 values. This was an entirely different data set than the many used by Tifft. Thus there is no 'small' data set, but a series or rather large ones. Every time a data set has been increased in size, the anomaly becomes more prominent, as Danny mentioned.
When Guthrie and Napier's material was statistically treated by a Fourier analysis a very prominent "spike" emerged in the power spectrum, which supported redshift quantization at very high confidence level. The initial study was done with a smaller data set and submitted to Astronomy and Astrophysics. The referees asked them to repeat the analysis with another set of galaxies. They did so, and the same quantization figure emerged clearly from the data, as it did from both data sets combined. As a result, their full analysis was accepted and the paper published. It appears that the full data set was large enough to convince the referees and the editor that there was a genuine effect being observed - a conclusion that other publications acknowledged by reporting the results.
As far as the effect on cosmology is concerned I need only point out the response of J. Peebles, a cosmologist from Princeton University. He is quoted as saying "I'm not being dogmatic and saying it cannot happen, but if it does, it's a real shocker." M. Disney, a galaxy specialist from the University of Wales is reported as saying that if the redshift was indeed quantized "It would mean abandoning a great deal of present research." [Science Frontiers, No. 105, May-June 1996]. For that reason, this topic inevitably generates much heat, but it would be nice if the light that inevitably comes out of it could also be appreciated. (Barry Setterfield, March 7, 2002).
Barry Setterfield answers Robert Day
In response to Day's 1997 criticism posted to the Talk.Origins Archive website
© 2000 Barry Setterfield. All Rights Reserved. [Last Modified: 10 March 2002]
An article written by Robert P. J. Day, copyrighted 1997, has been posted for some time on the Talk Origins Archive. This article purports to debunk my research regarding the speed of light. However, except for one lone sentence, the entire essay is based on a series of progress reports that preceded the August 1987 paper written at the request of Stanford Research Institute. For Day to prefer to critique, in 1997, articles representative only of work in progress even before the Report itself was published (ten years before Day's article was copyrighted) shows how inappropriate his methods of research and criticism are.
The only statement that Robert Day has made that has any real relevance to the current discussion over c-decay is his mention of the Acts and Facts Impact article for June 1988 issued by Gerald Aardsma for the ICR. Aardsma's incorrect methodology was pointed out to him by several individuals before he even published the article. He arguments were also effectively rebutted by Trevor Norman, who was in the Math Dept. of Flinders University. Norman's rebuttal was based on a superior statistical approach recommended by the then Professor of Statistics in his Department. Aardsma never fully addressed the issues raised by Norman, and neither did several other statistical detractors. Furthermore, following an extensive series of analyses, Alan Montgomery presented two articles, one at a Creationist Conference (ICC 1994 Proceedings), the other in Galilean Electrodynamics (Vol.4 No.5 [1993] p93 and following), that effectively silenced all statistical criticism of the c-decay proposition. Montgomery's two articles have never been refuted.
Day's criticism of my acknowledgment of my presuppositions is interesting. Is he decrying my honesty or the presuppositions themselves? He is welcome to disagree with them, but in return I would ask him to admit his own presuppositions, which I find I disagree with. As a Christian I do accept God's Word, or Scripture, as authoritative on the issues it addresses. Thus it is reasonable that I would be interested in pursuing an area of research which addresses some of these matters. I am not infallible and do not claim to have all the facts here. But the same situation prevails in any field of scientific endeavor, and that is why research continues. In the meantime, progress in data collection, observational evidence, and subsequent updating of a theory is very different from Day's mockery of a person's faith. I am wondering if his mockery may be a last resort when the legitimate scientific criticism was effectively answered long before the copyright date of 1997 on Day's article.
It should also be noted that a number of qualified scientists who do not share my beliefs have also come to a similar conclusion to mine. Not only have Moffat, Albrecht and Magueijo and others pointed out that the speed of light was significantly higher in the past, but Barrow has also suggested that it may still be continuing to change. This is a current, and open, field of research, and I encourage Day to read material more up to date than that which was published in the 1980's.
In the meantime, my work is still continuing on other aspects of the topic. In line with work done by Tifft, Van Flandern, Puthoff, Troitskii, and a number of other researchers, it appears that there is some solid evidence in space itself regarding the changing speed of light. This is the subject of a paper completed this year which has been submitted to a physics journal for peer review. Others from both evolution and creation backgrounds are also continuing research regarding the changing speed of light. As a result, c-decay is alive and well, and Robert Day's dismissal of the proposition appears to be somewhat premature.
Barry Setterfield, August 2000.
Question: Light Speed and Pleochroic Halos
Recently I have been reading up on some of Barry Setterfield's speed of light work and became puzzled again on an issue. I brought this question up a little while back but didn't get much of a reply. Considering I'm still puzzled I thought I'd ask the question again.
From Setterfield's page I read the following: "If conservation laws are valid, a slow-down in c, measured dynamically, should be matched by a proportional change in electron orbit velocities and other atomic processes" (http://www.setterfield.org/report/report.html#2a).
This made me rethink Robert Gentry's work with Polonium Halos embedded in granites around the world.
If the speed of light was much faster at the moment of creation.....Would the rate at which polonium atoms emit radioactive particles increase? (half life decrease)
Would this then change the KeV of the polonium atom? If the KeV of each decaying particle increases, would the emitted radioactive particles go farther and then etch the granite in a proportional yet larger halo? If the speed of light was faster at the moment of creation would the speed of the particle also be quicker and go farther also creating a larger halo?
I ask the question because I was wondering if there is a contradiction between Gentry's and Setterfield's work. If I'm incorrect...in my assumption... and the halos would be unaffected by the speed of light and no contradiction between the work of Gentry and Setterfield, is there someone who could present an explanation as to why?
Response: First of all, although the speed of light was higher and the rate of radioactive decay faster, the total energies involved were still constant. However, because the energy in all atomic processes is conserved regardless of the speed of light this means that atomic masses, such as those of electrons, would be lower proportional to 1/c2. The energy of emission of a particle is therefore constant, but because the masses of those particles were lower the initial velocity of that particle would be higher.
I explained this in Ex Nihilo, vol. 4, no. 3, 1981: "Many involved in radiometric dating of rocks would maintain that Pleochroic halos provide evidence that the decay constants have not changed. Crystals of mica and other minerals from igneous or metamorphic rock often contain minute quantities of other minerals with uranium or thorium in them. The alpha particles emitted by the disintegrating elements interact with the host material until they finally stop. This produces discoloration of the host material. The distance that the alpha particles travel is dependent firstly upon their kinetic energy. As the binding energy for a given radioactive nuclide is constant, despite changing c, so also is the energy of the emitted alpha particle. This arises since the alpha particle mass is proportional to 1/c2. But its velocity of ejection is proportion to c. Thus, as kinetic energy is given by (mv2), it follows that this is constant. As the alpha particle moves through its host material, it will have to interact with the same number of energy potential wells which will have the same effect upon the alpha particle energy as now. ÊIn other words the alpha particle's energy will run out at the same position in the host material independent of the value of c.
"It might be argued, however, that the alpha particle's velocity of ejection is proportional to c so it should carry further. This is not the case, as a moments thought will reveal. Another reason that the particle slows up is that the charge it carries interacts with the charges on the surrounding atoms in the host material. In the past, with a higher value of c, the alpha particle mass was lower, proportional to 1/c2. This results in a situation where the effective charge per alpha particle mass is increased by a factor of c2. In other words, the same charge will attract or repel the lower mass much more readily. Consequently, the slowing effect due to interaction of charges is increased in proportion to c2 exactly counteracting the effects of the mass decrease proportional to 1/c2, which resulted in the higher velocity. That is, the radii of the Pleochroic halos formed by ejected alpha particles will remain generally constant for all c." (Barry 8/10/03)
Question: What is the main stream of thinking about radioactive dating among creationists today? Comments from the ICR RATE group seem to indicate that they now believe that at some time in the past, radioactive decay was accelerated in comparison to current decay rates. I think that the CDK school of thought implies accelerated decay, but what about the other creation thinking?
Response from Helen Setterfield: First, the term 'decay' for radioactive changes is an unfortunate one, as it is associated with Romans 8. It's different altogether. It is this same radioactive 'decay' which lights up the stars! So yes, it was there from the moment God said 'Let there be light!'
Secondly, it had a great deal to do with the Flood of Noah, but not because of the rapid rate of radioactive decay then. Something that is often either forgotten or ignored by young earth creationists is that the short half-life elements were decaying also at the beginning! When this is considered in combination with the evidence which has arisen that radioactive elements on earth started out well underneath the crust, we have a source of incredible heating going on inside the earth from the very start.
There is an indication of this in Genesis 2 -- the earth was watered by mists or streams or water of some form coming up from the ground. Water does not go 'up' unless it is under pressure. Eden itself is listed as the source of headwaters for four rivers (which indicates, by the way, that it must have been on some kind of rise). In other words, the waters were already under pressure from the beginning.
As the heating continued, more and more water was driven out of the subcrustal rocks. The critical point was reached in Genesis 7:11 when ALL the fountains of the deep BURST at the same time, initiating the Deluge.
The faster speed of light did NOT cause faster radioactive decay. This is a misconception Barry faces constantly. The speed of light and radioactive decay are both the results of a primary cause -- like being children of the same parents. But they do not have a cause and effect relationship with each other.
The criticism I have of the RATE material right now is that there seems to be a desire to have a sudden, unexplained, increase in decay rate at specific times, which then fits their presuppositions. But perhaps it is more important to follow the data. One of the interesting things which came as a complete surprise to Barry, but which should have been expected, is that the clumping of radiometric dates (and yes, they are clumped) very closely matches the clumping of the quantized redshifts. The material is presented briefly here:
http://www.setterfield.org/quantumredshift.htm#periodicitiesandgeo
I apologize for the formatting problems. This particular paper has been a bugaboo...we are trying to get a lot of the stuff sorted out, but I think that the chart in that section should help explain what Barry is referring to. The decay rate of radiometric materials was indeed much faster in the past. As it turns out, which is confirmed by that chart, it tracks almost exactly with the redshift curve, so that we can see how fast it was before. The redshift curve is the same curve as the light speed curve and also the same curve as the fitting of orbital dates with atomic, or radiometric, dates. The curve can be found here:
http://www.setterfield.org/cdkcurve.html For those of you familiar with equations, please know that the equation shown on the chart is based on a constant speed of light -- it is the standard equation for redshift, as I recall. However when criticized regarding this, Barry sat down and worked out the equation in a completely different way but ended up coming up with almost exactly the same curve. I think the new paper may have some of that; I don't know. I'll ask him about it when he gets here and see if we can't get it up on his website.
His articles on a Brief Earth History and a Brief Stellar History cover this stuff quite clearly, I think. Neither is terribly long and at least they will help the reader know the basics of what the Setterfield model is about and why it is that way. (12/14/03) (For more recent discussion and more details see Barry's discussion page--Ed.)
Comment: Looking at this from a geologic standpoint, it doesn't seem likely that the watering would be done by means of a spring or a shallow aquifer, since, without rainfall (or some other means, I suppose) to provide recharge, it's not likely there would be enough hydraulic head to produce springs or any significant flow from an aquifer - at least not for very long. However, if a surface water body were nearby and weather conditions were right, that could produce a very wet morning fog or mist that could provide enough moisture to water the vegetation. I'm assuming that there would need to be some fresh water sources nearby to provide for the needs of Adam and his family, as well as the various animals and indeed Genesis 2:10-14 does mention four rivers which were divided from one river which flowed out of Eden. Since rivers usually flow into one another as tributaries and not the other way around, I am wondering if this could mean that the main river flowed into a lake or some other body of water and then divided into the four rivers. I can't really envision any other way for this to work. This surface water body could then be the source of the mist or fog that watered the vegetation. Now I know that a body of surface water is not mentioned, but how else are you going to get four substantial rivers from a one river source?
Response from Helen Setterfield: You are a geologist. You know that a good portion of the earth's mantle is now olivine. Olivine is nothing but serpentine with the water driven out of it heat being the most likely suspect here.
This is from Barry's essay on the geological history of the earth:
"Some meteorites are taken to represent samples of material from the formation of the solar system and hence the Earth. For example, carbonaceous chondrites, may hold more than 20% water locked up in their mineral structures [6]. More specifically, carbonaceous chondrites of class CI are made up of hydrated silicates as well as the volatile components water, carbon dioxide, oxygen and nitrogen [7]. By way of an earthly example, the beautiful mineral serpentine is a hydrated silicate that contains 12.9% water in its composition [8]. Upon heating, this water is given up and the mineral turns to olivine, thereby reducing its volume [9]. Interestingly, olivine is an important component of the earth's mantle. In a similar way, other hydrated silicates, found in meteorites and on earth, may give up their water content when heated sufficiently, with a consequent reduction in volume. Indeed, the chondrules within the chondrite meteorites themselves are silicate spherules that have been melted and the volatile water component driven off. The remaining minerals in the chondrules contain a prominent amount of olivine [10].
The Role of Radioactive Decay: After creation week, the interior of the earth began to heat up from the rapid decay of short half-life radioactive elements as a result of high light-speed values. This radioactive heating drove the water out of serpentine, and other minerals in the mantle, towards the earth's surface. This water came to the surface as springs and geysers and watered the ground. This is confirmed by the earliest known translation of the Pentateuch, the Septuagint (LXX), that originated about 285 BC [11], and from which the Patriarchal dates in this Summary are taken. The LXX specifically states in Genesis 2:6 that "fountains" sprang up from the ground. These fountains and springs probably watered the whole landmass of the single super-continent that made up the original land surface of the earth. In the surrounding ocean, this continuing water supply was called the "fountains of the deep." On a greatly reduced scale, a similar phenomenon still occurs today with the "black smokers" of the South-East Pacific Rise." http://www.setterfield.org/earlyhist.html
It is the heating which produced the water. We are still bombarded by asteroids and meteorites which are considered to have the original rock composition of the solar system's inner planets. A lot of serpentine there.
The very heating that produced the springs/mists of Genesis 2 also produced the massive bursting of Genesis 7:11. Later on, the rocks themselves started melting, producing the pools of magma underneath which produced an age of volcanism which is very evident in the geologic record and which is NOT part of any flood. This heating also continued driving water out of the rocks which, when mixed with the magma produced the asthenosphere, across which the earth's crustal plates slid with such force and suddenness that Peleg and his brother Joktan were both named in memory of those terrifying years. The asthenosphere isn't quite as slippery now, as the heating has diffused enough to stabilize our continents except for the temblors and occasional major earthquakes but these are nothing like the days of Peleg.
It was the interior heating due to the decay of both long and short half-life elements together which was the contributing factor to ALL of this.
Dating Jericho
I am curious. I have read your chronology concerning the time
from the destruction of the Jewish temple to the Creation of the
Universe. You say that this happened about 5,792 B.C. Now, looking
at Jericho, as just one example, archaeological evidence (?) claims
that this city was founded in about 10,000 B.C., or even earlier.
Now, I believe in God, and I fully believe in Creation: that God
Created the Heavens and the Earth, and He did so in 7 days. I
have no doubt about that. Just to get that fully understood.
I'm curious about why these dates don't correspond.
In addition, I have seen other dates. The domestication of dogs
and sheep happened about 10,000 B.C. I have also read that the
first controlled and purposeful use of fire was about that same
time. In addition, metal work developed around that same time.
These are all dates that I have seen a number of places! . Granted,
they were developed in an evolutionary time-scale, I am still
rather con fussed, and would like to know what you think. I have
not done a full and complete analysis of Genesis dates, as you
have, but through these various points, I had come to the conclusion
that the Creation had occurred around 10,000 B.C. I was also thinking
(using about 2,000 years) that the flood had occurred about 8,000
B.C., and that the growth and development of humanity, from a
tribal group (as they must have been coming off of the ark) into
urban societies had taken about that long - up to about 5,000
B.C.
I am also curious about the table II, presented in the 'Creation
and Catastrophe Chronology'. The last two columns are titled
"Atomic Time BP at Patriarch's Birth" and "Light
Speed (times present value)". I am very curious about what
exactly you mean by those two columns. The values given in those
two columns are wide! y variable (one starts in the multi-billions,
the other in the tens of millions). Those are some very large
jumps.
As stated above, I fully believe that God Created the Earth and
the Universe. I'm not questioning that. I'm not even questioning
your papers. I'm simply trying to understand the differences that
I've observed. The dates that I've drawn upon - while utilizing
secular information - seem to be too coincidental for mere happenstance.
However, the time scale that you propose in your papers seems
to be exceedingly logical and straightforward. In addition, they
draw upon information that comes from the Bible (either from the
OT (MT version) or the older LXX version).
Response from Barry Setterfield (January 16, 2004): First,
about Jericho and the older civilizations: there are two main
ways of trying to figure out dates: artifacts and radiometric
dates. When pottery or other artifact types resemble each other
but are in different layers, we have an ambivalent situation.
This ambivalence also occurs when we have similar artifact types
in two cultures that are distant from each other. Thus carbon
dating is often resorted to.
We can get RELATIVE chronologies (this culture existed before
that culture because we find it below the second one) from sites
without much trouble, but getting POSITIVE dates according to
our calendars is much more difficult. Written records are
an enormous help, when they exist. We can often correlate a known
event historically with a written mention of it in some records.
But this is not the common case. Therefore it is common practice
to use radiocarbon dating as something by which an absolute standard
and date can be set.
Thus the assignment of ten thousand years BC to various events
is an estimate based on a form of dating which is not accurate
past about six or seven thousand years! Claims that it is
accurate to about forty thousand years have no way of verifying
that claim the only verification we can have of historical
dates is in known historical events, and we must calibrate off
them. There are no known historical events occurring before
approximately 4000 B.C. possibly even as recently at 3000
B.C. The rest depends on the accuracy of dating techniques, of
which radiocarbon dating is the least accurate of all the radiometric
dating types.
With that said, it has to be acknowledged that radiometric dates
of all sorts give ancient very ancient ages. The
chart you are referring to as being confusing, Luke, is one which
is the result of the work which was done to correct one set of
dates with the other. The work involves measurements taken by
physicists over the years regarding something called "atomic
constants." These govern the rate of radio decay in heavy
elements. I became fascinated over twenty years ago with the
fact that, contrary to what I was taught in physics courses in
university, a number of these 'constants' were not constant at
all, but were changing. This led me to the fields I have been
studying since then.
It is imperative to recognize that these 'constants' are the numbers
used to determine the rates of decay for various elements. If
these constants were not constant, but changing, then so was the
rate of radio decay, which means our assessment of these ancient
dates was in error. How to correct this discrepancy was not really
evident until other work done by astronomers, actually, in the
1990's and continuing today. Below I have linked a number of
my papers which might help explain it to you, but the final conclusion
is that when we take a look at something called 'the redshift
curve' and take into account that, astronomically, distance equals
time (the further out you look, the further back in time you are
also looking), we can get a correction factor which lines up the
atomic dates derived from radiometric dating and the dates we
use on our calendars, which depend on the orbiting of the earth
around the sun and the moon around the earth. It is the
result of that correction factor which you are seeing in the chart
you find confusing.
The redshift curve is here: http://www.setterfield.org/cdkcurve.html

This curve also indicates the changing speed of light through
time, as both the redshift and light speed have the same parent
cause. Light speed is one of the elements of all radio decay
rate equations, which means that when the speed of light was faster,
so was the decay rate. If you look at that curve, over on
the left, you will see how incredibly fast the speed of light
was at the beginning compared to now, and this correlates to how
fast radio decay was immediately after creation compared to now.
When we deal with a normal, or orbital time line in comparison
to that, we get the chart you have referred to.
Now, about the actual age of the earth this is presented
fairly clearly when one links the chronologies of the Bible, especially
as dating back from known events, which is what I have done here:
http://www.setterfield.org/scriptchron.htm.
Keep in mind the Bible mentions two things which may cause you
to pause in some of your (very worthwhile) mental meanderings.
First, in Genesis 4 we learn that metallurgy had been established.
However, and secondly, no traces of this would be left
after the flood except in the memory of the skills which the residents
of the Ark must have had. So any archaeological finds 'dating'
from 10,000 B.C. are erroneous. Does this make sense for you?
You are caught, as all of us have been, in trying to decide which
carries the most weight: man's interpretations or biblical statements.
I came down, finally, on the side of biblical statements not
only because my own research revealed the data all pointed in
that direction, but because the Bible is an interwoven series
of documents which holds together, even to presentation of the
ages. This must be taken into account, for the minute we
start rearranging one part of Genesis with currently-held scientific
opinion, other parts of the Bible start to fall as well. It does
come as a unit, and I'm sure your studies will lead you to see
that as you go.
You are doing a good job. You are thinking and studying and taking
God's Word seriously. No one could ask for more. Keep it up
and God bless you and guide you in your efforts. We are always
Question: I have come across some interesting research by Col. Tom Bearden, a systems analyst. He has written a book called "Energy From the Vacuum". And he also has a website. it is http://www.cheniere.org. This is a more detailed explanation of how the system works. He says that he puts in 1 unit of energy and gets 100 units out.
Response from Barry: The postings on the topic about energy from the vacuum, its origin, and Colonel Bearden's claimed extraction of that energy, deserve five pertinent comments.
First, while Col. Bearden has several patents to his credit, some of his ideas may not be correct. A colleague and good friend of mine in Australia is well versed in Bearden's work and previously believed he was credible. My colleague has been an employee of some of the power supply companies in Australia, but was extremely interested in alternative power sources because of the limitations of our present power systems. Consequently, he was interested in what Bearden had to offer and has personally corresponded with Bearden in an effort to replicate his results. He spent some time faithfully constructing equipment and circuits according to Bearden's specifications, but has been unable to reproduce Bearden's claimed results. This has been a bitter disappointment to my colleague since he started off with high expectations.
Second, the existence of the vacuum Zero Point Energy (ZPE) is generally accepted by the scientific community. There are several ways in which the presence of this ZPE (which exists as electromagnetic waves of all wavelengths) can be shown to exist. One of these is the Casimir effect, named after Henrik Casimir, the Dutch physicist who anticipated its existence in the 1940's. In this instance, two metal plates are brought very close together in a vacuum. In line with theory, any two such plates will only allow to exist between them electromagnetic waves whose wavelengths are a sub-multiple of their distance apart. In other words, the plates effectively exclude all the long wavelengths. As a result, those excluded wavelengths outside the plates exert a radiation pressure which forces the plates together. In 1997 and 1998, this Casimir force had its existence re-confirmed experimentally, but this time with an accuracy that fully supports the theory. In fact, in reporting the results of this experiment, New Scientist titled the article "Fifty years on and the force is with us at last." (25 January 1997, p. 16)
This leads on to the third point about the extraction of power from the ZPE. While Bearden has claimed this, my colleague's experience leads to some doubts on this matter. Furthermore, NASA has been subsidizing research in this area in order to derive a power source for possible future spacecraft. A number of symposia have taken place under their auspices on this matter. Basically, the Casimir effect or some variation of it has been the only successful proposition, and because of the minute scale on which it operates, the power extracted is minuscule, and the system is not one where efficiency is greater than 100%, despite Bearden's claims. Bearden's suggestion, then, that the established order is not likely to explore the possibility of such energy extraction is incorrect. One report, for instance, having to do with this is B. Haisch, A. Rueda and H. E. Puthoff, AIAA Paper 98-3143, given at 34th Conference of American Institute of Aeronautics and Astronautics, July 13-15, 1998, Cleveland Ohio. Also to be referenced:
1. Daniel C. Cole and Harold E. Puthoff, "Extracting energy and heat from the vacuum", Physical Review E, volume 48, number 2, 1993, pp 1562-1565.
2. H. E. Puthoff, Ph.D., "Can the Vacuum be Engineered for Spaceflight Applications? Overview of Theory and Experiments", NASA Breakthrough Propulsion Physics Workshop, August 12-14, 1997, NASA Lewis Research Center, Cleveland, Ohio
Fourth, Dave Bradbury mentioned that the existence of the ZPE was only partially understood.' Some comment is necessary here. There have been two theories concerning the origin of the ZPE. One claims that the " sum of all particle motions throughout the Universe generates the zero-point fields" and that in turn " the zero-point fields drive the motion of all particles of matter in the Universe - as a self-regenerating cosmological feedback cycle." [New Scientist, 2 December 1989, p.14]. Several papers have capably demonstrated that this mechanism can maintain the presence of the ZPE once it had formed, but this avoids the question of its origin, since it was shown in 1987 that the ZPE is required to maintain atomic structures and atomic motion across the cosmos. Thus it becomes difficult to envisage how these atomic structures emerged in the first place by the feedback mechanism. The other school of thought is that the ZPE was arbitrarily fixed at the birth of the cosmos as a part of its boundary conditions.
It is this second proposal that several of us have explored in some detail and leads to the fifth comment. This has resulted in a paper entitled " The Redshift and the Zero Point Energy" which is co-authored by myself and Daniel Dzimano. The paper has been published by the Journal of Theoretics and is available on their website in the extensive papers' section and can be found here: http://www.journaloftheoretics.com/Links/Papers/Setter.pdf
In this paper, we demonstrate that the processes operating to produce the ZPE will require the ZPE to build up with time. Furthermore, because the ZPE maintains atomic structures across the cosmos, the increase in the ZPE with time will allow all atomic orbits to take up higher energy values with time. Thus the light emitted from those orbits will be bluer with time, since the blue end of the spectrum is the high energy end. As a result, when we look back in time at distant astronomical objects, the light emitted from those atoms will be redder, and this is the origin of the redshift. Redshift quantization is predicted, and the size of the quantization is in good agreement with that observed by Tifft. The final piece of evidence that this paper provides is that the processes operating to build up the ZPE with time can be treated mathematically on the basis of known physical laws. When this is done, the redshift/distance relationship is reproduced, but in such a way that the observed deviations from the standard formula can be readily accounted for. Because the strength of the ZPE is the determining factor in the value of Planck's constant, h, the speed of light, c, and the rate of ticking of atomic clocks, the form of this curve also indicates the form of behavior of those quantities. (Barry Setterfield, 2/16/04)
Questions and Comments from an Astronomer: (1) Sanduleak -69 degrees 202 was a blue giant, and theory says that it is the red giants which are supposed to blow, not blue ones; and the progenitor star was not what we expected for a type II SN. However, this was an odd SN, fitting neither type I nor type II. For instance, the light curve was different. It is interesting that the first naked-eye SN since the invention of the telescope is unique. Still, the theory is that the core of the progenitor star collapsed.
(2) Creation Theory says the Universe is less than 10,000 years old, yet the travel time of the photons and neutrinos was supposedly 170,000 years. These two truths cannot be held simultaneously. This is the well-known light travel time theory, for which I don't think we have a satisfactory answer at this time.
(3) The special theory of relativity says it takes an infinite amount of energy to accelerate a particle with mass to the speed of light; how then can the SN 1987a photons and neutrinos arrive at essentially the time? Current neutrino theory says that neutrinos have mass. Neutrino mass is very low. With such small mass, neutrinos can travel very close to the speed of light, so as I understand it, even with a 170,000 light year distance, this is not a problem. At the time of the SN (1987), I thought that this disproved neutrino mass, but a discussion with a friend of mine who at the time did high energy astrophysics convinced me otherwise.
Replies from Barry Setterfield: The statement is made that SN 1987a was a blue giant, and theory says that it is the red giants which are supposed to explode, not blue ones.
In response I refer to some statements by the late Sir Fred Hoyle, who was one of the prime originators of the theory of stellar aging. He writes: "Stars explode when the mass of the core exceeds Chandrasekhar's limit [1.44 times the mass of our sun, so] supernovae may be expected to occur in cases where the total mass [of the star] only slightly exceeds the limit - these are cases where the explosion occurs in the late stages of the evolutionary track [of a star]...The extent of evolution [of a star] is determined by the fraction of the mass of the star that comes to reside in the core. The explosion point, on the other hand, is determined by the total mass in the core, quite regardless of what fraction of the star's mass this happens to be. Evidently, a star of mass 1.5 times the Sun will not explode until almost the whole mass comes to reside in the core. Hence such a star does not explode until it reaches a late stage of its evolution. But a star of mass 15 times the Sun will explode when only about 10 per cent of its hydrogen has been consumed. Such a star would therefore be disintegrated at almost the beginning of its evolutionary track. For a star to evolve appreciably [off] the main sequence its mass should not exceed about 6 times the Sun." [Fred Hoyle, Frontiers of Astronomy, pp.218-220, William Heinemann Ltd, London, 1956].
Under these conditions, it would seem that blue giants such as the progenitor of SN 1987a, could easily be candidates for such explosions. It may also be that the designation of supernovae into Type I and Type II is too restrictive, and that SN 1987a is broadening our classification possibilities in line with Hoyle's original proposals.
Question 2 concerns the distance to SN 1987a which is about 170,000 light years. In other words, light traveling at its present speed would take 170,000 years to reach us from this object.
As the inquirer has pointed out, this poses a problem for those who maintain an age for the whole universe of less than 10,000 years. However, there have been encouraging developments from several lines of inquiry. Our own investigation of this matter has indicated that the answer seems to lay in the changing properties of the vacuum, namely the Zero Point Energy (ZPE).
The presence of the ZPE is accepted by the vast majority of physicists and its existence and strength has been proven by experiment, observation and theory. Some of this evidence and further details about the ZPE can be found in our article "Exploring the Vacuum" published by the Journal of Theoretics (http://www.journaloftheoretics.com/Links/Papers/Setterfield.pdf). It is considered that the strength of the ZPE is uniform throughout the cosmos. As Max Planck pointed out in 1911, Planck's constant, h, is a measure of the strength of the ZPE. But there is an additional factor. Our own research indicates that five observational anomalies can be very simply resolved if the strength of the ZPE has increased with time. The first anomaly is Planck's constant, h, itself. The officially declared values of h have increased with time in line with experimental evidence. This suggests that the strength of the ZPE has also increased with time. The second anomaly is that light speed has been measured as decreasing with time. The third anomaly is that atomic masses have been measured as increasing with time. The fourth anomaly is that the rate of ticking of atomic clocks has slowed compared with the dynamical or orbital standard. The final anomaly is the redshift and its quantization which has been measured by comparing the redshifts of galaxies in the same cluster. The data for the first four anomalies have been documented in "The Atomic Constants, Light. and Time" by Norman and Setterfield (http://www.setterfield.org/report/report.html). The data on the redshift are in the extensive astronomical literature.
In other words, the increase with time of one physical quantity, the ZPE, can account for five anomalies which would otherwise be inexplicable on modern scientific theory. The strength of the ZPE is related to the stretching of the cosmos during Creation Week. In the same way that stretching a rubber band or inflating a balloon puts energy into the fabric of the rubber band or balloon, so the stretching of the heavens put energy into the fabric of space. This energy appears as the ZPE. In our Journal of Theoretics article entitled "The Redshift and the Zero Point Energy" (http://www.journaloftheoretics.com/Links/Papers/Setter.pdf), the origin of the ZPE from this stretching process is considered in detail, and the reason for the increasing strength of the ZPE elucidated and treated mathematically. There Dr. Daniel Dzimano and I show that the build-up of the strength of the ZPE with time follows an equation with the same characteristics as the redshift/distance or, what amounts to the same thing, redshift/time relationship. This means that all five anomalies are behaving in a way that is dictated by this same equation.
When the necessary conversion factors are inserted in accord with observation, it turns out that light can reach earth from the most distant parts of the cosmos in less than 10,000 years. The reason why light speed decreases with an increase in the strength of the ZPE is that an increase in the strength of the ZPE effectively means that the electric permittivity and magnetic permeability of free space also increases. Since these two quantities govern light speed via an inverse relationship, it follows that light speed must slow if the ZPE increases. Details about this can be found in the two articles in the Journal of Theoretics.
Question 3: The same issue puzzled me. If anyone has any further information, I would be grateful.