Cosmology
One of the important features of the General Theory of Relativity is its application at a "Global" level. The analysis of gravity can be applied to the universe as a whole. The universe can be assumed to be a relatively homogeneous distribution of matter and energy.
For a distributed mass such as a cloud of gas or the universe as a whole:
![]() ….(42)
….(42)
where r = mass density
V = volume of integration
According to the mass – energy equivalence principle, the energy density ![]() can be related to a mass density.
can be related to a mass density.
Thus:
![]() …..(43)
…..(43)
Integrating over a sphere of radius R(t) gives:
![]() ……(44)
……(44)
Now at the surface of a sphere the acceleration due to gravity is given by:
![]()
So ![]() ….(45)
….(45)
If we assume that the universe is bounded and of radius R(t) then the acceleration of the universe will be:
![]()
Thus ![]()
Or ![]() ……(46)
……(46)
According to this equation, the universe can not be static. If it began at a fixed size, we should observe the universe getting smaller (Note the negative sign on the right hand side).
What we do observe is that the universe is not contracting, but expanding. Therefore either:
- This equation is incomplete and requires another positive term to counter the effects of gravitational attraction.
- The universe exploded into existence at some time in the past, using some mechanism which is no longer in operation and is even now decelerating in accordance with this equation.
Einstein made the first assumption. Thus equation (46) becomes:
![]() ….(47)
….(47)
Where ![]() = cosmological constant.
= cosmological constant.
Now ![]()
And 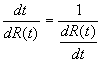
Thus 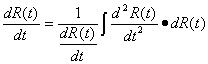
So ![]() …..(48)
…..(48)
![]()
![]()
Or 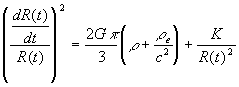 ……(49)
……(49)
Now, if the universe is bounded it means that nothing can escape from this universe, nor enter it. Therefore, the mass and energy of the universe is fixed. But if the radius of the universe is changing with time we note that the density of the mass energy of the universe has changed with time.
![]() ….(50)
….(50)
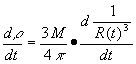
Now ![]()
Therefore ![]() … (51)
… (51)
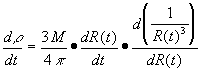
![]()
Substituting from equation (50) gives:
![]()
or 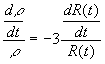 …(52)
…(52)
Now 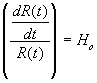 where Ho is the Hubble expansion constant.
where Ho is the Hubble expansion constant.
As R(t) becomes very large, ![]()
Now the "classic approach" to this problem shows that equation (52) has a solution when ![]() where t is the expansion time of the universe, thus
where t is the expansion time of the universe, thus 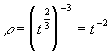 .
.
However, as most mathematics students will know it is impossible to have a single solution for two unknowns with only one equation. In fact there is no single solution to equation (52). Let us explore the "classic approach" first and consider the implications of it. Then let us consider a more realistic solution.
The Classic Solution
Substituting into equation (49) and assuming that both K and ![]() = 0 gives:
= 0 gives:
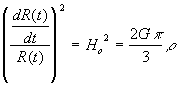 …..(53)
…..(53)
Substituting for density gives:
![]()
Rearranging gives:
![]()
Or
![]() …..(54)
…..(54)
Note: Ho has been measured to be between 40 to 100 km s-1 Mpc-1 (Mpc is a mega parsec = 3 x 1022 m). In more standard units this is between 1.33 x 10-18 m s-1 m-1 and 3.33 x 10-18 m s-1 m-1
Knowing that G is 6.670 x 10-11 m kg-1 s-1 and substituting into equation (54) gives a range of expansion times for the universe between 8.89 x 1012 and 3.55 x 1012 seconds.
A Different Approach
Let us revisit the solution to equation (52). In fact, a more realistic approach would be to say that equation (52) has a solution when ![]() where t is the expansion time of the universe and "n" can be any value, thus
where t is the expansion time of the universe and "n" can be any value, thus 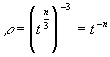 .
.
Substituting into equation (49) and assuming that both K and ![]() = 0 gives:
= 0 gives:
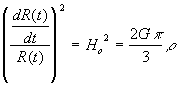 …..(53)
…..(53)
Substituting for density gives:
![]()
Rearranging gives:
![]()
Or
![]() …..(54)
…..(54)
Note: Now, "n" can be any number, but for convenience let us consider it being a positive integer. Knowing that Ho is between 1.33 x 10-18 m s-1 m-1 and 3.33 x 10-18 m s-1 m-1 and G is 6.670 x 10-11 m kg-1 s-1 we can calculate a range of expansion ages for the universe depending on the value of "n".
| Value on "n" | Ho = 3.33 x 10-18 | Ho = 1.33 x 10-18 |
|---|---|---|
| 1 | t = 1.258 x 1025 s | t = 7.88 x 1025 s |
| 2 | t = 3.55 x 1012 s | t = 8.88 x 1012 s |
| 3 | t = 2.32 x 108 s | t = 4.29 x 108 s |
| 4 | t = 1.88 x 106 s | t = 2.98 x 106 s |
Implications of This Theory
By this stage, the reader should have realised that from special relativity it can be shown that matter and energy are equivalent and from general relativity it can be shown that space and time are equivalent.
The underlying feature of the mathematics is "equivalence".
Maxwell had already shown that electricity and magnetism were equivalent. Now Einstein had shown that mass, energy, space and time were also equivalent. It seems reasonable to assume that there should be further equivalence in the universe.
Unified Field Theory
Realising the possibility of further "equivalence" in nature, one of the major efforts of modern physics is the search for the "Unified Field Theory". This is an attempt to condense all known "field" like forces of gravity, electromagnetic phenomenon, weak and strong nuclear forces into one single equation.
Extra Dimensions
One of the not so obvious features of Einstein's work was the possible existence of further dimensions in the universe.
Consider the problem of curvature of the space-time system. It is difficult to visualise curvature of three-dimensional space, but it is easier to visualise the curvature of two-dimensional spaces. For example, a piece of paper can be used to represent a two dimensional space system. If the piece of paper is laid out flat, we say that it has "no curvature". This would correspond to our three dimensional space with no matter in it.
However, if the piece of paper is wrapped around into a cylinder, then it has "curvature". The radius of this curvature is the radius of the cylinder formed from the piece of paper. However, this radius must be measured in a third dimension. Similarly, if our three dimensional space is curved as predicted by Einstein's equations, there must exist a fourth "space like" dimension which has not been discussed as yet. (Note this is not the time).
Note: If our piece of paper was inhabited by two dimensional beings, they would be restricted to the surface of their paper world and would not be able to make any direct measurements of the third dimension. At best they could measure the parameters of their piece of paper and deduce that a third dimension may exist and determine the radius of curvature of their world in this third dimension. Similarly, we may not measure this fourth dimension of space directly, but may deduce its existence, and some of its properties.
So, Einstein's work points to the existence of five dimensions (at least), four space like dimensions and time.
Space-Time has a Beginning
Another not so obvious feature of Einstein's work, when taken in conjunction with other work done by Hubble (1920's) on the movement of galaxies is the prospect that we live in an expanding universe.
Over a four-year period, starting in 1966, George Ellis, Stephen Hawking, and Roger Penrose affirmed that any universe governed by general relativity that is expanding and that contains at least some matter and energy must possess a singular origin in the finite past. But they went farther. They discovered that the operation of general relativity guarantees a singular boundary not just for matter and energy but also for space and time.
Consider:
If the universe is expanding, it is reasonable to assume that if we were to reverse the process the universe would contract to a point. The only problem with this is that if all the matter of the universe were to contract onto itself at some point it would form a black hole with an event horizon. Therefore if all the matter in the universe began at a point and expanded into Pre-existent space it would encounter this event horizon and not be able to expand any further. Calculations have shown that the universe is considerably larger than the diameter of its corresponding event horizon, therefore one of two things has happened:
- The universe has in fact expanded out of a black hole into pre-existent space in spite of the problems of mathematics this may cause. This means that our concept of time in the universe should be seriously reconsidered. For example, matter which emerged from the event horizon early in the universe's history would be incredibly old compared to that matter which emerged later, simply due to the time distortions associated with an event horizon itself.
- That space and time are the parameters which have expanded, thus avoiding some of the event horizon problems, and that matter is simply "along for the ride" in expanding space. In other words, if general relativity does accurately describe the physics of the universe, both the stuff that makes up the universe and the dimensions in which that stuff exists and operates share a common origin. This finding is called the space-time theorem of general relativity.
In 1970, however, that crucial if still hung over general relativity. Expansion was no longer in doubt; the existence of matter and energy never had been in doubt. And though the operation of general relativity had been affirmed— to one percent precision (two decimal places) it had not yet been established with adequate certainty to put theoreticians' doubts to rest. By 1980, the level of certainty had improved to better than a hundredth percent precision (four decimal places, impressive, and yet still not quite enough to satisfy the most skeptical. But in 1993, the lingering shred of uncertainty finally flew away.
The Nobel Prize in physics that year went to Russell Hulse and Joseph Taylor for their twenty-year-long study of the binary pulsar PSR 1913+16. This stellar system is unique: two neutron stars (one of which is also a pulsar) orbit closely about one another. Through their study of this system in which gravitational forces exceed those seen in our solar system by hundreds of thousands of times, Hulse and Taylor were able to affirm the accuracy of general relativity to better than a trillionth percent precision (that is, to fourteen decimal places). In Penrose's words, Hulse and Taylor's work "makes Einstein’s general relativity, in this particular sense, the most accurately tested theory known to science!"
Mathematical Breakthrough Solves String Problem
In the latter weeks of 1994, while people around the world prepared to celebrate Christmas, physicists Ed Witten and Nathan Seiberg gave their own special gift to humanity. They reduced an entire field of mathematics to a single short paper. For decades mathematicians were stymied in their attempts to describe, with precision, certain physical phenomena requiring four-dimensional space. Their equations seemed impossible to solve, even with super computers. But a pair of super brains did it. Witten and Seiberg transformed these extremely complex equations into simple ones, almost as simple as the calculus equations with which undergraduates work.
String theorists recognized almost immediately that they had just received a boost toward success in their endeavors, but even the optimists assumed that deciphering a workable theory would take at least a few more years of hard work. To their surprise and joy, the crucial breakthrough came in a matter of months.
Witten and Sieberg helped by eliminating an annoying physical absurdity from super-symmetry theory. When Witten and Sieberg introduced a hypothetical massive particle that has the potential to become massless, the absurdity vanished. Taking a clue from this approach, physicist Andrew Strominger proposed a certain type of blackhole, what he calls a "charged extremal black hole," as the possible solution to a similar problem encountered in string theory. Later, Strominger teamed up with physicist Brian Greene and mathematician David Morrison to demonstrate that charged extremal black holes can transform into fundamental particles, and vice versa, in a manner similar to ice turning into liquid water and liquid water into ice.
As an unexpected bonus, Strominger, Greene, and Morrison found that by introducing such transformations, the ten thousand plus different string theories operating in four, five, six, and ten space dimensions could all be united with perfect consistency into just one theory, the ten-dimensional one.
Massless Black Holes?
As most students of science and viewers of Star Trek realize, a black hole has so much mass that its gravity pulls in anything —even light—that gets close enough to it. But, in order for Strominger’s blackholes to fit neatly into string theory, black holes must become massless at critical moments. This necessity raises an obvious question: How can a black hole have zero mass without violating the definition of a black hole or, more difficult yet, without violating the principles of gravity? Simply put, how can there be gravity without mass?
The answer was found in the spatial configuration of a black hole in extra dimensions. Strominger discovered that in six space dimensions, the mass of a particular black hole (an "extremal" black hole, one with a mass and charge so tiny as to be comparable to one of the fundamental particles) is proportional to its surface area. By making this area small enough, eventually the mass becomes zero. To answer the question another way, special relativity tells us mass and energy are interchangeable. General relativity extends this principle to space and time. When spatial lines are curled up tightly enough, mass and space become interchangeable also. For the tiny black holes Strominger is describing, the space curvature is certainly tight enough to accomplish this interchangeability. Black holes, which never fitted into string theory before, now do fit in a way that actually solves string theory’s most perplexing problems.
Detailed analysis of the mathematics behind Relativity and its extensions (String Theory) show us that space, time, mass and energy are all essentially the same and that, at the very beginning, the universe consisted of "nothing". The universe has a finite history and came into existence suddenly.
Conclusion
The existence of higher dimensions can not be proven at this point in time --the required atomic accelerator energy levels are well beyond present technology. Therefore we can not be sure that they are really there. "Elegance" and "beauty" and "simpler equations" are attractive reasons for favoring a new theoretical model but they are not infallible guidelines. Not everything that meets these aesthetic criteria describes the world as it really is. However, the possibility of higher dimensions could explain some very disturbing results from Quantum Theory such as the famous "Two Slit Experiment", which indicates that two particles can influence one another at a distance, instantaneously.